profile pic
⌘ '
raccourcis clavier
Search

Convolutional Neural Network

  • Étiquette

    • publié à

    • modifié à

    • durée

      1 min de lecture

    • source

      llms.txt

    See also: this one assignment on CNN

    how can we exploit sparsity and locality?

    think of sparse connectivity rather than full connectivity

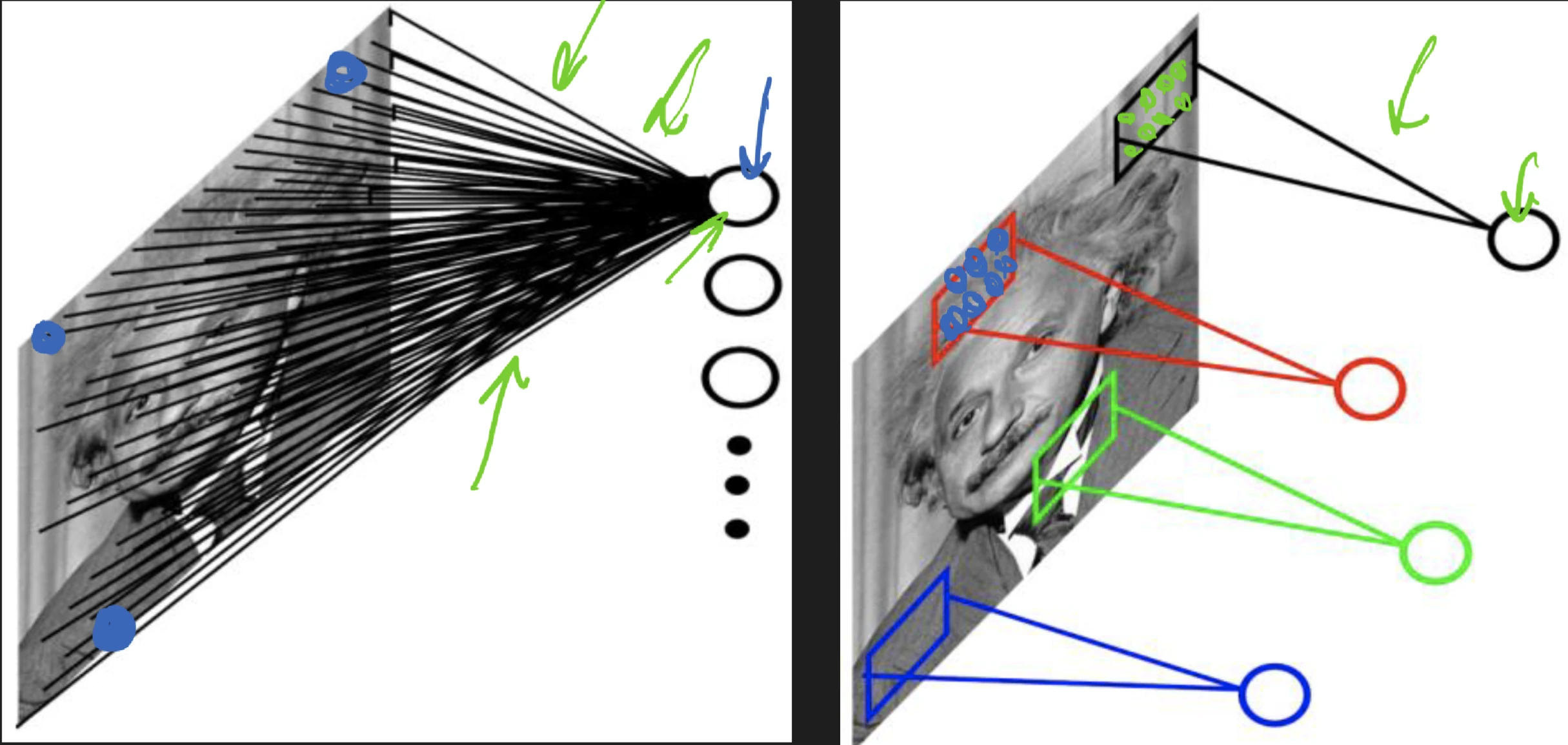
    where we exploiting invariance, it might be useful in other parts of the image as well

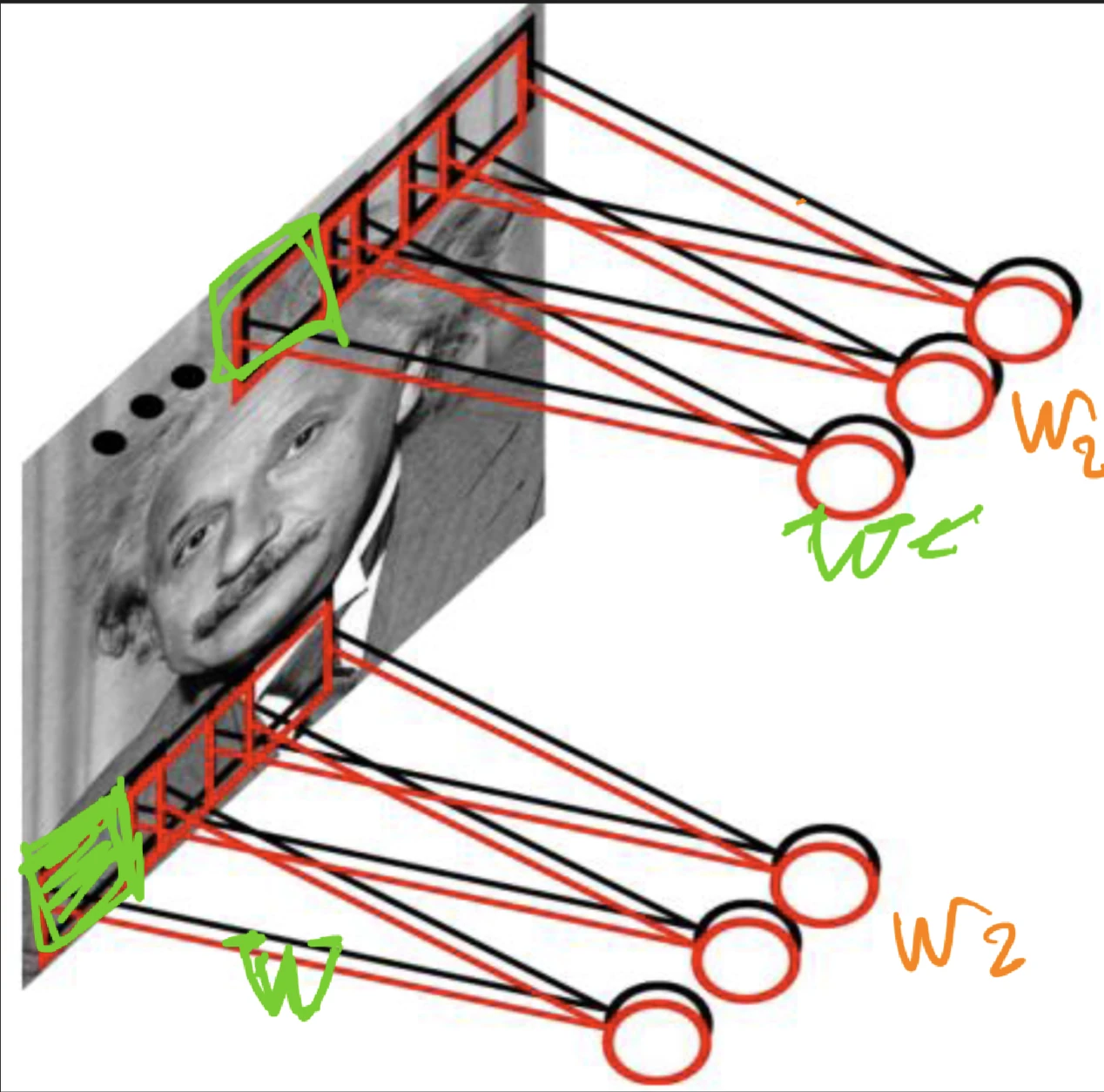
    convolution

    accept volume of size W1×H1×D1W_1 \times H_1 \times D_1 with four hyperparameters

    • filters KK
    • spatial extent FF
    • stride SS
    • amount of zero padding PP

    calculation

    produces a volume of size W2×H2×D2W_2 \times H_2 \times D_2 where:

    • W2=W1−F+2PS+1W_2 = \frac{W_1 - F + 2P}{S} + 1
    • H2=H1−F+2PS+1H_2 = \frac{H_1 - F + 2P}{S} + 1
    • D2=KD_2 = K

    1D convolution:

    y=(x∗w)y(i)=∑tx(t)w(i−t)\begin{aligned} y &= (x*w) \\ y(i) &= \sum_{t}x(t)w(i-t) \end{aligned}

    2D convolution:

    y=(x∗w)y(i,j)=∑t1∑t2x(t1,t2)w(i−t1,j−t2)\begin{aligned} y &= (x*w) \\ y(i,j) &= \sum_{t_1} \sum_{t_2} x(t_1, t_2) w(i-t_1,j-t_2) \end{aligned}

    max pooling

    idea to reduce number of parameters

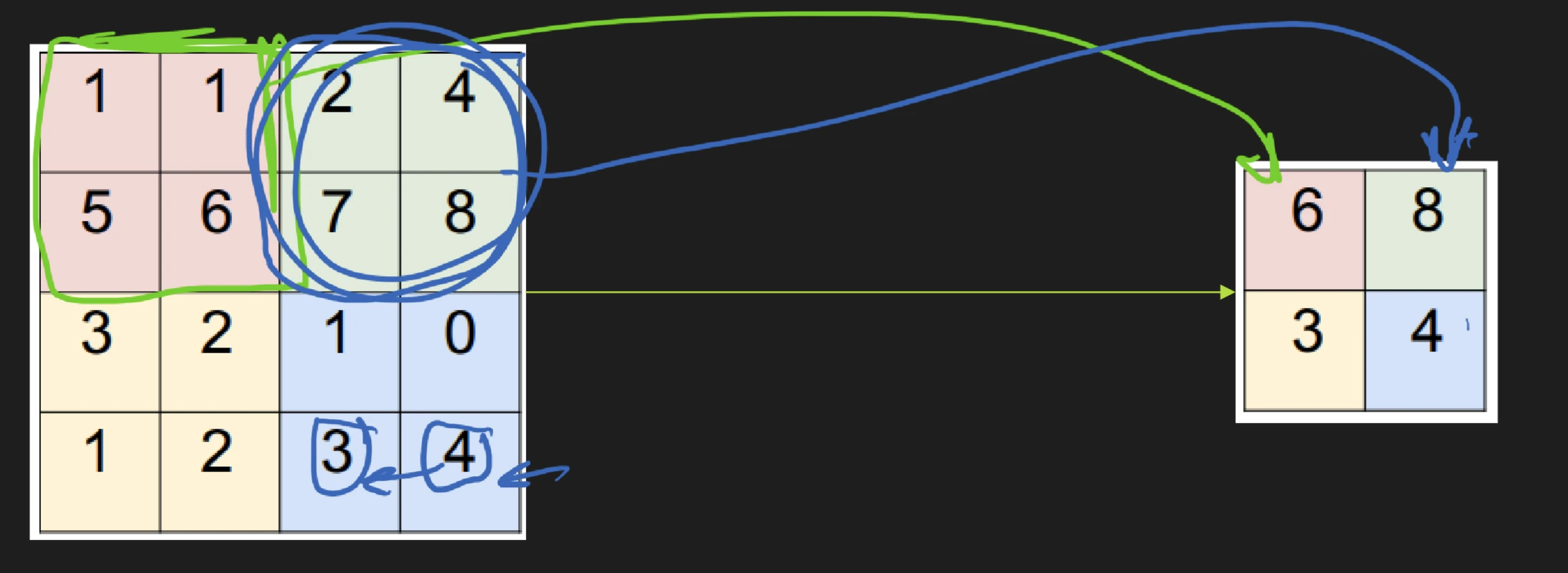
    batchnorm

    xj=[x1j,…,xdj]x^{j} = [x_1^j,\ldots,x_d^j]

    Batch X=[(x1)T…(xb)T]TX = [(x^1)^T \ldots (x^b)^T]^T

    Vous pourriez aimer ce qui suit

  • No free lunch
  • distraction
  • databases internals
  • friendship
  • Orwellian
  • Lighting
  • XLA
    • Machine learning
    Detects pattern within data and use it to make useful prediction. Generally AI \subset ML \subset DL Some main exploration: Transformers Large language models NLP CNN Logistic regression Optimization gradient descent hyperparameter tuning ensemble learning Recommender systems Reinforcement learning Q-learning Policy Gradient Monte-Carlo Tree Search Generative Models GAN VAE Autoencoder sparse autoencoder sparse crosscoders Supervised Q-learning Low-rank adapters Fields mechanistic interpretability Related: linear algebra.
    Connectionist networks
    and an unstructured overview of patterns in machine learning