Solar systems in the context of exoplanets

Ref: Solar System Exoplanets 2024

Obj.

• content of solar system and orbital properties
• Compare properties of Solar System to known exoplanetary
• six techniques for exoplanet detection & limitation.

---

How people learn?

Student enter the classroom with preconceptions about how the world works. If their initial understanding is not fully engaged, they may fail to grasp new concepts

develop competence

1. foundation knowledge
2. interrelationships among facts and concepts
3. retrieval and application.

Solar system

Sun → terrestrial planets → asteroid belt → Jovian (gas giants) ~ Ice giant planets → Trans-Neptunian objects (TNOs) (Dwarf planets → Kuiper belt → Oort cloud)

1 au (astronomical unit): average distance between Earth and Sun

Planetary orbits are (nearly) co-planar

• Dispersion in mutual inclinations: $\Delta{i} \approx 2\text{ deg}$
• Pluto and many other TNOs are _more highly inclined

Consequence of Protoplanetary disks

from Alma telescope

• radio images of warm dust continuum ($\leq 10^6\text{ Myrs}$)
• Disk sizes $\approx 100\text{ au}$
• Variety of morphologies

Question

Concentric gaps opened by protoplanets?

• Due to active construction of two protoplanets?

Question

What other dynamical properties do you expect for planets formed from a disk?

• Keplerian Motion: Planets formed from a disk are expected to exhibit Keplerian motion → direct consequence rather than properties

Regular vs. Irregular Satellites (aka, moons)

Regular Satellites	Irregular
Resemble mini planetary systems	Irregular orbits
prograde	prograde or retrograde orbits
low mutual inclinations, e.g: 4 Galilean moons of Jupyter	highly elliptical
nearly circular orbits	highly inclined

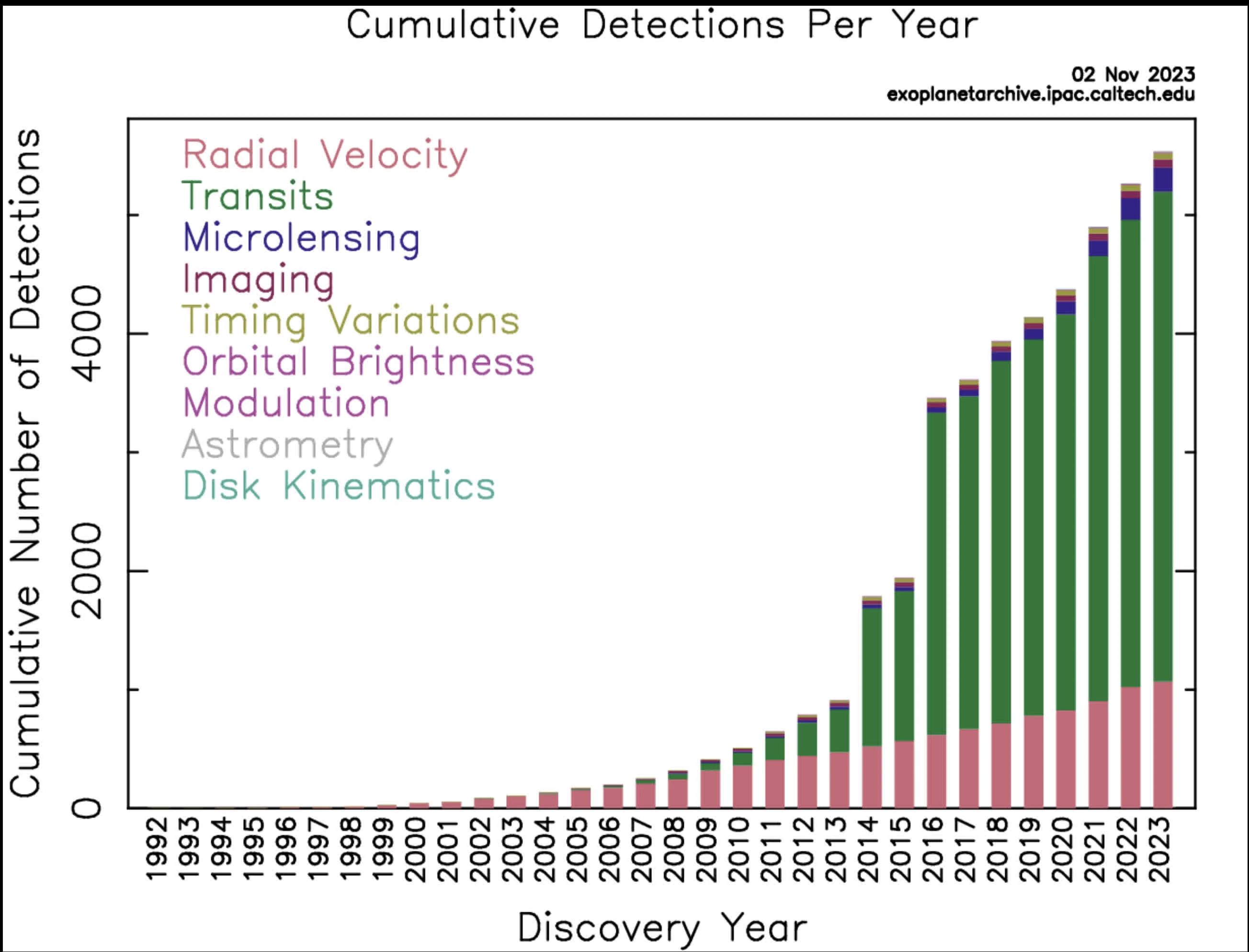
Most exoplanetary systems are compact

Kepler-11 System

Transit

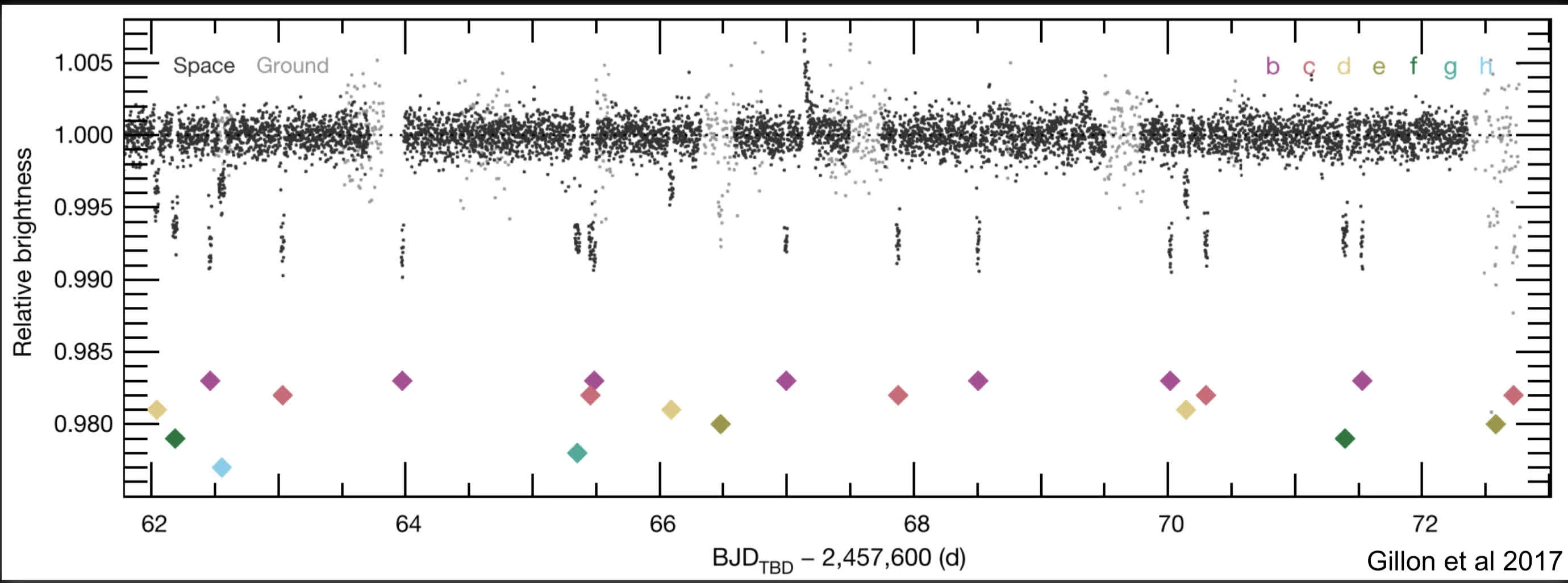
• Time-resolved photometry (i.e. stellar brightness) = “light curve” Can measure:
• Orbital period
• Orbital inclination
  • Has to be edged-on
  • relative to telescope, not to the star
  • Reference is line-of-sight to exoplanetary system.
• Planet radius

transit depth.

$$\begin{aligned} \mathbf{Z} &= \frac{\text{Area}_{pl}}{\text{Area}_{*}} = (\frac{R_{pl}}{R_*})^2 \\\ &\\\ Z&: \text{transit depth} \\\ R_{pl}&: \text{planet radius} \\\ R_{*}&: \text{stellar radius} \\\ \end{aligned}$$

limb-darkening

• appears fainter at their edges compared to centres
• depends on the star’s temperature structure and the wavelength of the observations

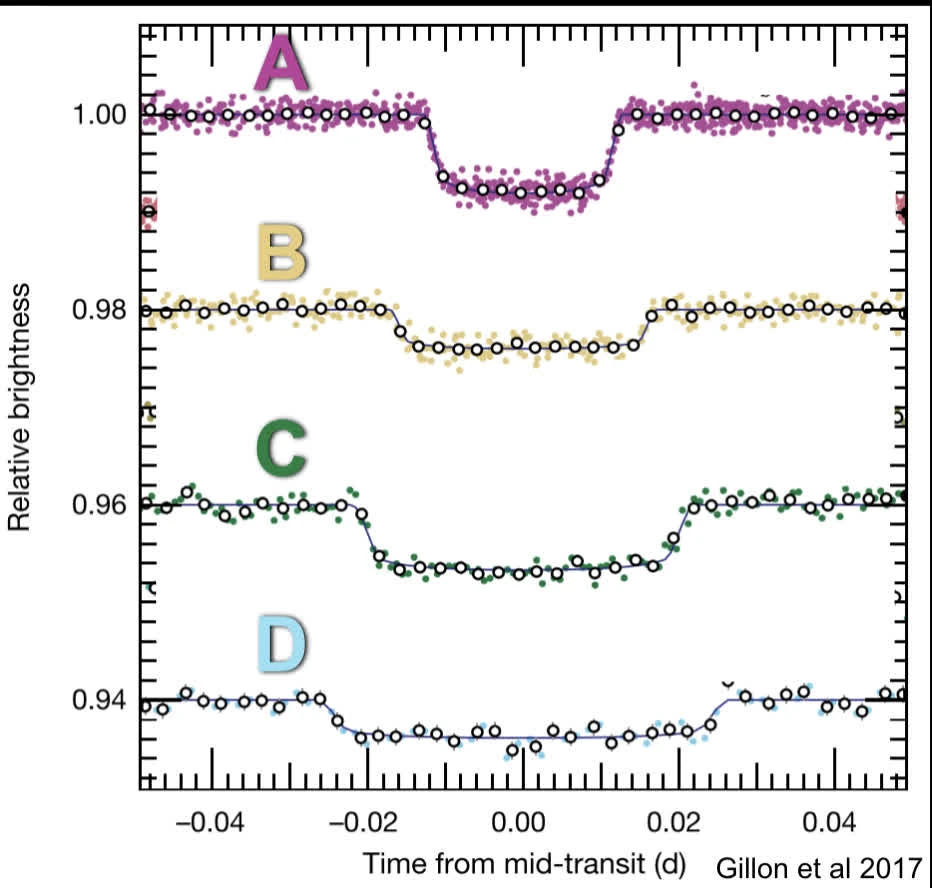
The higher the depth, the larger the planet

Limb-darkening only depends on the stars, and wavelength observing at

Depth doesn’t depends on how far away the planets is away from the star (depends on the durations, orbiting more slowly)

Duration is impacted by period and inclination

known transiting expolanets

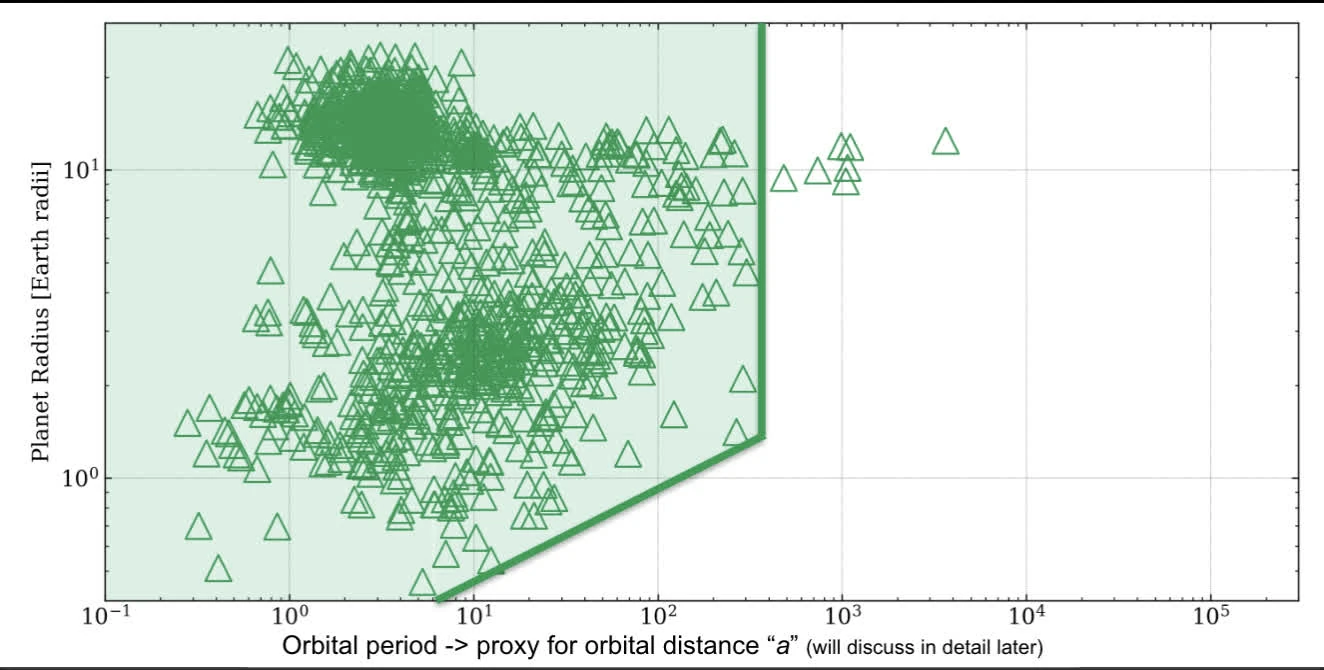
Geometric transit probability:

$$\begin{align*} P_{tr} &\approx \frac{R_{*}}{a} \\ &= 0.5\% \left( \frac{R_{*}}{R_{\odot}} \right) \left( \frac{a}{a_{\oplus}} \right)^{-1} \end{align*}$$

where $\odot$ and $\oplus$ is the sun and earth respectively

Transit Timing Variations

oscillating orbits

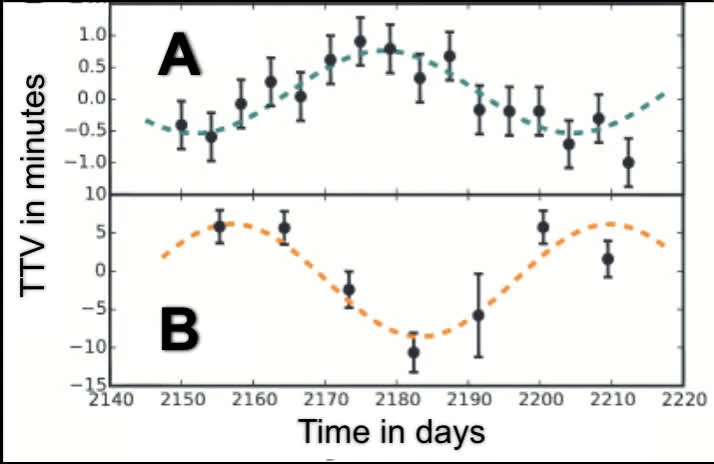
B exhibits larger TTV

A is more massive, since B is influenced by A (pulled by gravitational effect)

Radial velocity

Only sees the bigger stars chemical abundances in star atmosphere → graphs (dotted vertical lines)

Time-resolved spectroscopy to measure Doppler-shifted spectral features

Radial velocity shift translates into wavelength shift

$$\frac{\lambda_{obs}}{\lambda_{ref}} = \sqrt{\frac{1+v_{rad}/c}{1-v_{rad}/c}}$$

Can measure

• Orbital period
• Orbital eccentricity
• Planet’s minimum mass

semi-amplitude of RV signal K

K depends on the orbital inclination i such that RV method is sensitive an upper limit on planetary mass

$$\begin{align} K &= M_p(\frac{2\pi{G}}{PM_{*}^{2}})^{1/3} \\\ K &= M_p \sin{i} (\frac{2\pi{G}}{PM_{*}^{2}})^{1/3} \end{align}$$

Derivation

$$\begin{align} a_sM_s &= a_pM_p \\\ P^2 &= \frac{4\pi^2}{GM_{*}}a_p^3 \end{align}$$

$M_p$: planet mass, $i$: orbital inclination, $P$: orbital period, $M_{*}$: stellar mass

• Insensitive to face-on, maximally sensitive to edge-on
• Easier to detect big planets

Transits + Radial Velocity (Radius + mass) → planet bulk density

Astrometry

proper motions

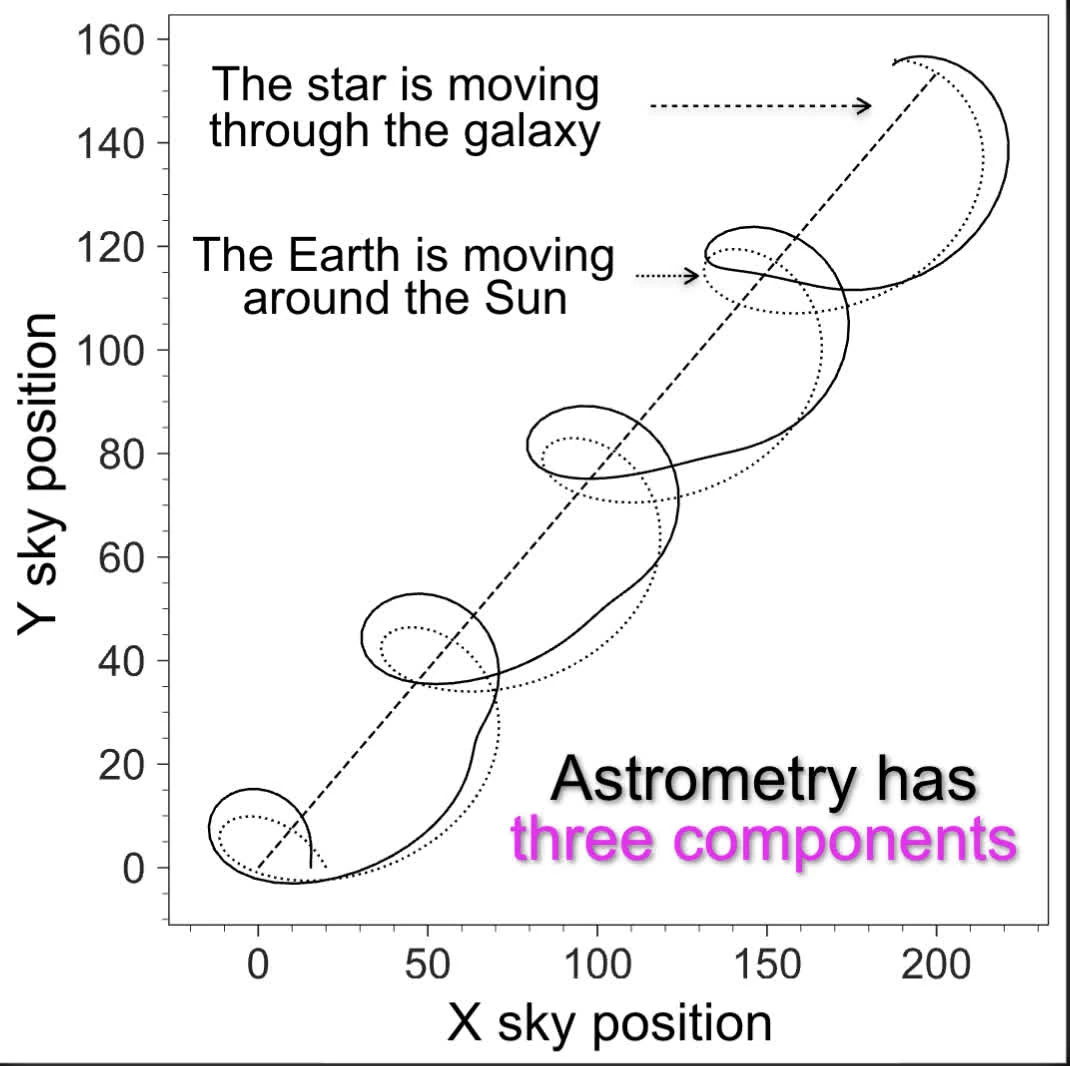
Aside - Parallax

1 pc = 1 AU / 1" 1” arcsec = 1/60 arcminutes = (1/60)/60 degrees

parsec is the distance from two planets

Consider a star-planet system located at d from us

$x=d\theta = 1{AU}(\frac{d}{1pc})(\frac{\theta}{1"})$

$$\triangle{\theta} = \frac{M_p}{d}(\frac{GP^2}{4\pi^2M^2_{*}})^{1/3}$$

biased on long period

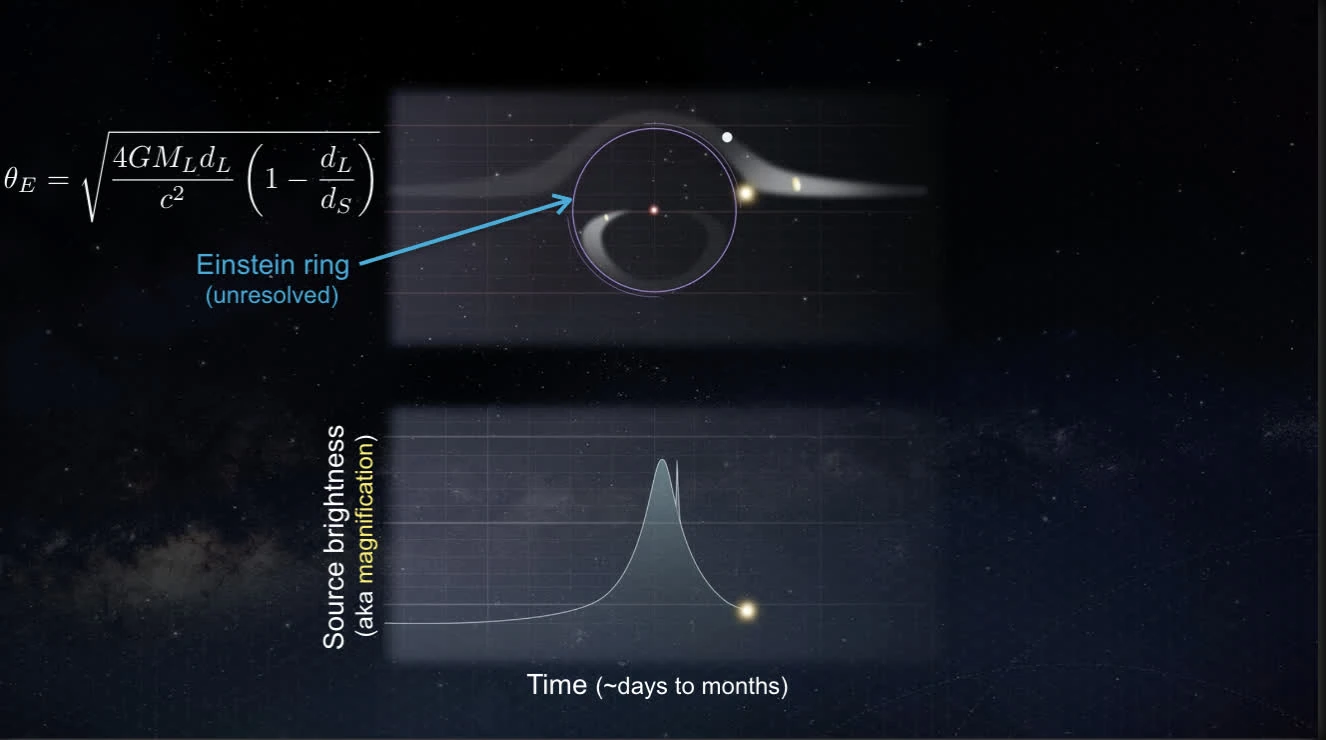
Gravitational Microlensing

Mass bends spacetime → light ray are bent by a curved spacetime → massive object act as gravitational lens