Context-free grammar and push-down Turing machine

Problème 1.

Give a context free grammar for the following language:

$$L=\{a^n{b}^m{c}^k\mid k\ne n+m\}$$

Solution

The following CFG generates the language $L$:

$$\begin{array}{rl}S& \to S_1\mid S_2\mid S_3\\ S_1& \to a{S}_{1}c\mid a{S}_1\mid A\\ S_2& \to b{S}_{2}c\mid b{S}_2\mid B\\ S_3& \to a{S}_{3}b\mid c{S}_3\mid C\\ A& \to aAc\mid aA\mid a\mid \epsilon \\ B& \to bBc\mid bB\mid b\mid \epsilon \\ C& \to aCb\mid cC\mid c\mid \epsilon \end{array}$$

Problème 2.

Let

$$L_1=\{a^n{b}^m{c}^k\mid n,m,k\ge 0\}$$

and let

$$L_2=\{a^n{b}^n{c}^n\mid n\ge 1\}$$

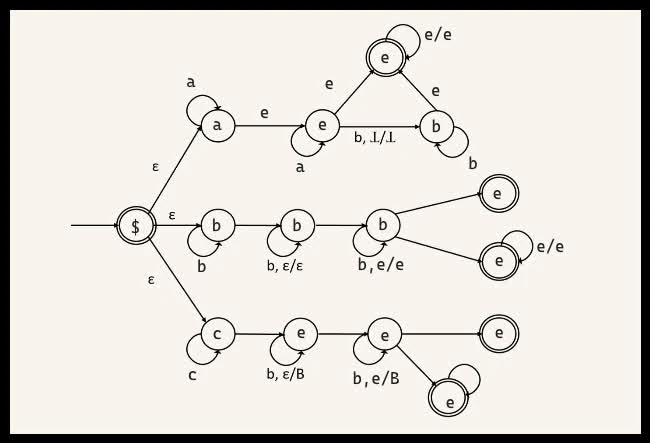
Complete the pushdown automata $M$ such that $L(M)=L_1-L_2$, where $\Sigma =\{a,b,c\}$.

Solution

Given that the $L(M)$ will accept all string where the number of a’s, b’s, and c’s are not all the same or there are zero of one or more types of characters, the following is the pushdown automata $M$

Problème 3.

The first table:

	1	0	x	#	c	$\square$
$q_s$	$(q_{1,1},x,R)$	$(q_{1,3},x,R)$	$(q_s,x,R)$	-	-	-
$q_{1,1}$	$(q_{1,1},1,R)$	$(q_{1,1},0,R)$	-	$(q_{1,2},\#,R)$	-	-
$q_{1,2}$	$(q_{1,5},x,R)$	==$(q_{1,2},x,R)$==	$(q_{1,2},x,R)$	-	-	-
$q_{1,3}$	$(q_{1,3},1,R)$	$(q_{1,3},0,R)$	-	$(q_{1,4},\#,R)$	-	-
$q_{1,4}$	==$(q_{1,3},c,L)$==	$(q_{1,7},x,R)$	$(q_{1,4},x,R)$	-	-	-
$q_{1,5}$	$(q_{1,5},1,R)$	$(q_{1,5},0,R)$	-	$(q_{1,8},\#,R)$	-	-
$q_{1,6}$	$(q_{1,6},1,R)$	$(q_{1,6},0,R)$	-	$(q_{1,9},\#,R)$	-	-
$q_{1,7}$	$(q_{1,7},1,R)$	$(q_{1,7},0,R)$	-	$(q_{1,10},\#,R)$	-	-
$q_{1,8}$	==$(q_{1,8},1,R)$==	==$(q_{1,8},1,R)$==	-	-	==$(q_{1,8},c,R)$==	==$(q_{1,end1},\square ,L)$==
$q_{1,9}$	==$(q_{1,9},1,R)$==	==$(q_{1,9},0,R)$==	-	-	==$(q_{1,9},1,R)$==	==$(q_{1,end2},\square ,L)$==
$q_{1,10}$	==$(q_{1,10},c,R)$==	==$(q_{1,10},1,R)$==	-	-	==$(q_{1,10},c,R)$==	==$(q_{1,end3},\square ,L)$==
$q_{1,end1}$	$(q_{1,end1},1,L)$	$(q_{1,end1},0,L)$	-	$(q_{1,end2},\#,L)$	$(q_{1,end1},c,L)$	-
$q_{1,end2}$	$(q_{1,end3},1,L)$	$(q_{1,end3},0,L)$	$(q_{1,end2},x,L)$	$(q_{1,end2},\#,L)$	-	-
$q_{1,end3}$	$(q_{1,end3},1,L)$	$(q_{1,end3},0,L)$	$(q_{1,end3},x,L)$	$(q_{1,end3},\#,L)$	-	$(q_2,s,\square ,R)$

The second table:

	1	0	x	#	c	$\square$
$q_{2,s}$	-	-	==$(q_{2,s},\square ,R)$==	==$(q_{2,1},\square ,R)$==	-	-
$q_{2,1}$	-	-	==$(q_{2,1},\square ,R)$==	==$(q_{2,1},\square ,R)$==	-	-
$q_{2,2}$	==$(q_{2,1},\square ,L)$==	==$(q_{2,1},\square ,L)$==	-	-	==$(q_{2,1},\square ,L)$==	$(q_{3,s},\square ,L)$

The final transition table:

	1	0	c	$\square$
$q_{3,s}$	$(q_{3,s},1,R)$	$(q_{3,s},0,R)$	$(q_{3,s},c,R)$	$(q_{3,1},\square ,R)$
$q_{3,1}$	$(q_{3,2},0,L)$	$(q_{3,2},1,L)$	$(q_{3,1},1,L)$	$(q_{3,2},\square ,R)$
$q_{3,2}$	$(q_{3,1},\square ,L)$	$(q_{3,1},\square ,L)$	$(q_{3,1},\square ,L)$	$(q_{3,end},\square ,L)$