---
date: '2024-02-09'
description: assignment on transfer functions of continuous-time systems with rlc circuit analysis using laplace domain, impedance calculations, and voltage divider rule.
id: content
modified: 2026-06-05 15:08:43 GMT-04:00
tags:
  - sfwr3dx4
title: Transfer functions of continuous-time systems
created: '2024-02-09'
published: '2024-02-09'
pageLayout: default
slug: thoughts/university/twenty-three-twenty-four/sfwr-3dx4/a1/content
permalink: https://aarnphm.xyz/thoughts/university/twenty-three-twenty-four/sfwr-3dx4/a1/content.md
generator:
  quartz: v4.6.0
  hostedProvider: Cloudflare
  baseUrl: aarnphm.xyz
full: https://aarnphm.xyz/llms-full.txt
---
**Problem 1**: Consider the following system:

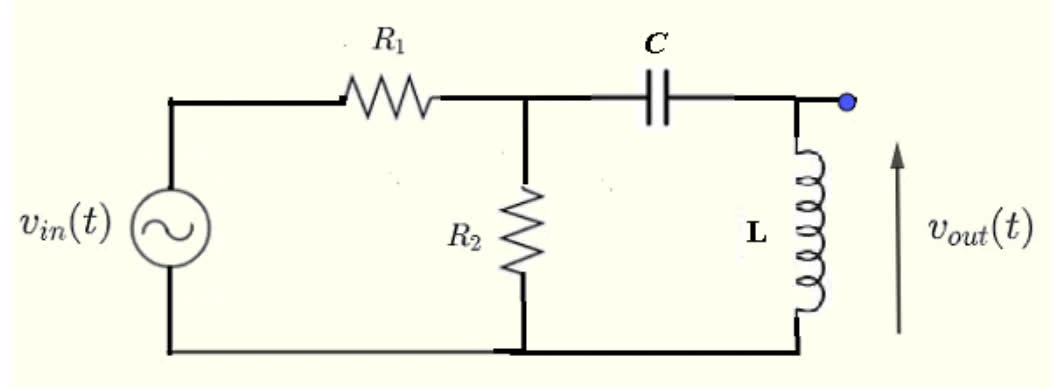![[thoughts/university/twenty-three-twenty-four/sfwr-3dx4/images/assignment-1-circuit.webp|assignment-1-circuit]]

Let $R_1 = 40\Omega, R_2 = 20\Omega, L = 10mH, C= 1\mu F$. The input is $v_{in}$ the output is $v_{out}$. Give both transfer function and state space representation for the system.

_Solution_

Given circuit is a second-order linear system due to presence of one inductor (L) and one capacitor (C).

Given transfer function $H(s)$ is given by the ratio over Laplace domain:

$$
H(s) = \frac{V_{out}(s)}{V_{in}(s)}
$$

Given that the impedance of the inductor $Z_l = sL$ and the impedance of the capacitor $Z_c = \frac{1}{sC}$, the total impedance of the circuit is given by:

$$
Z_{\text{total}} = \frac{1}{\frac{1}{sL} + sC}
$$

Using voltage divider rule, the transfer function is given by:

$$
H(s) = \frac{V_{out}(s)}{V_{in}(s)} = \frac{\frac{1}{sC}}{\frac{1}{sL} + \frac{1}{sC}}
$$

---