Root mean square

See also: pdf

problème 1.

The Root Mean Square (RMS) value of a signal $f(t)$ that is periodic with period $T$ is given by the equation $\sqrt{\frac{1}{T} \int_0^T{(f(t))^2dt}}$ It can be shown that the RMS value of $u(t) = B \sin{\omega t}$ is $\frac{B}{\sqrt{2}}$

1.a

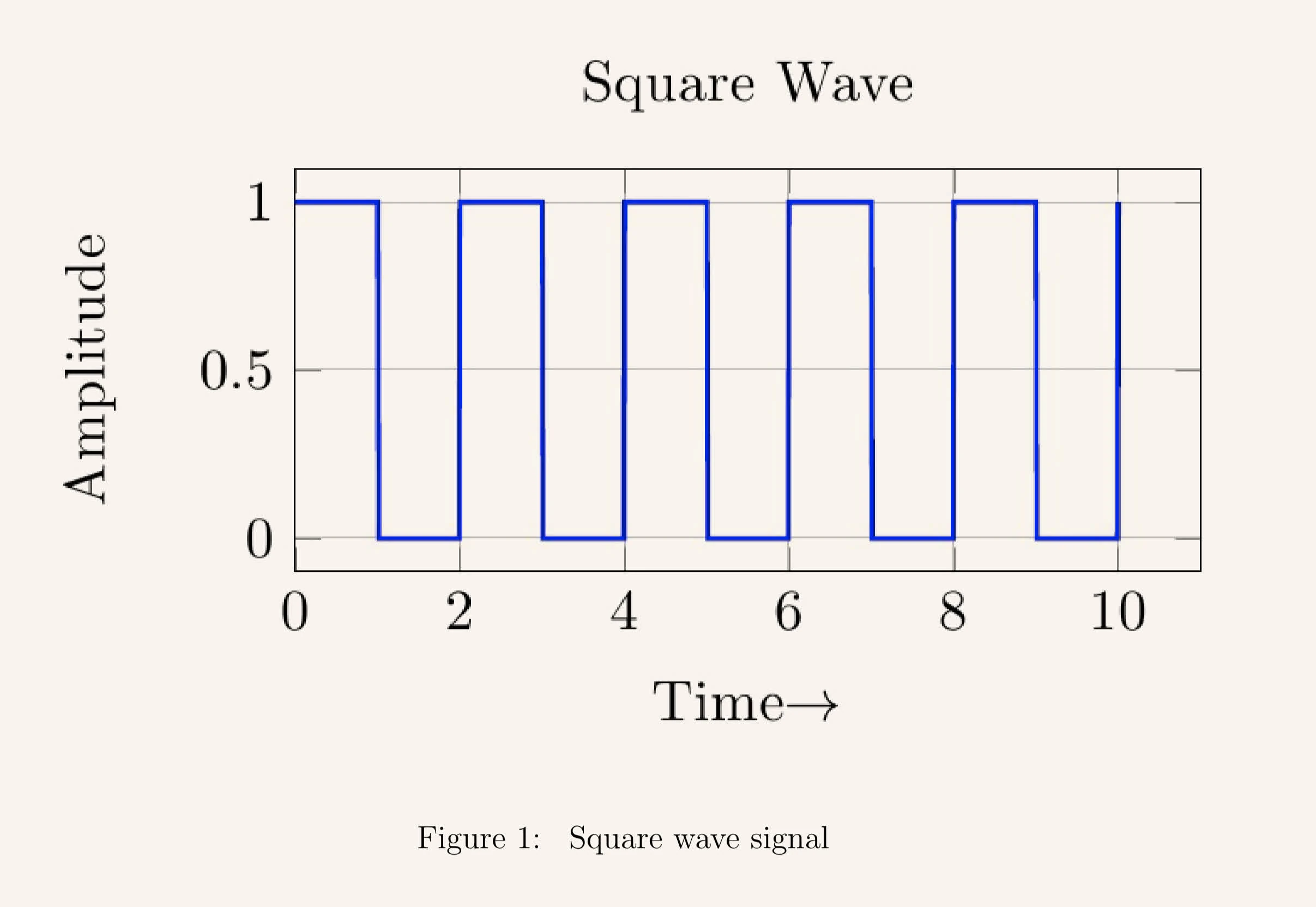
Square wave

The square wave function is defined as:

$$f(t) = \begin{cases} 1 & \text{if } 0 \leq t < \frac{T}{2} \\ 0 & \text{if } \frac{T}{2} \leq t < T \end{cases}$$

import sympy as sp
 
t = sp.symbols('t')
T = 2
 
RMS = sp.sqrt(1/T * sp.integrate(1, (t, 0, T/2)))

RMS = $\frac{1}{\sqrt{2}}$

1.b

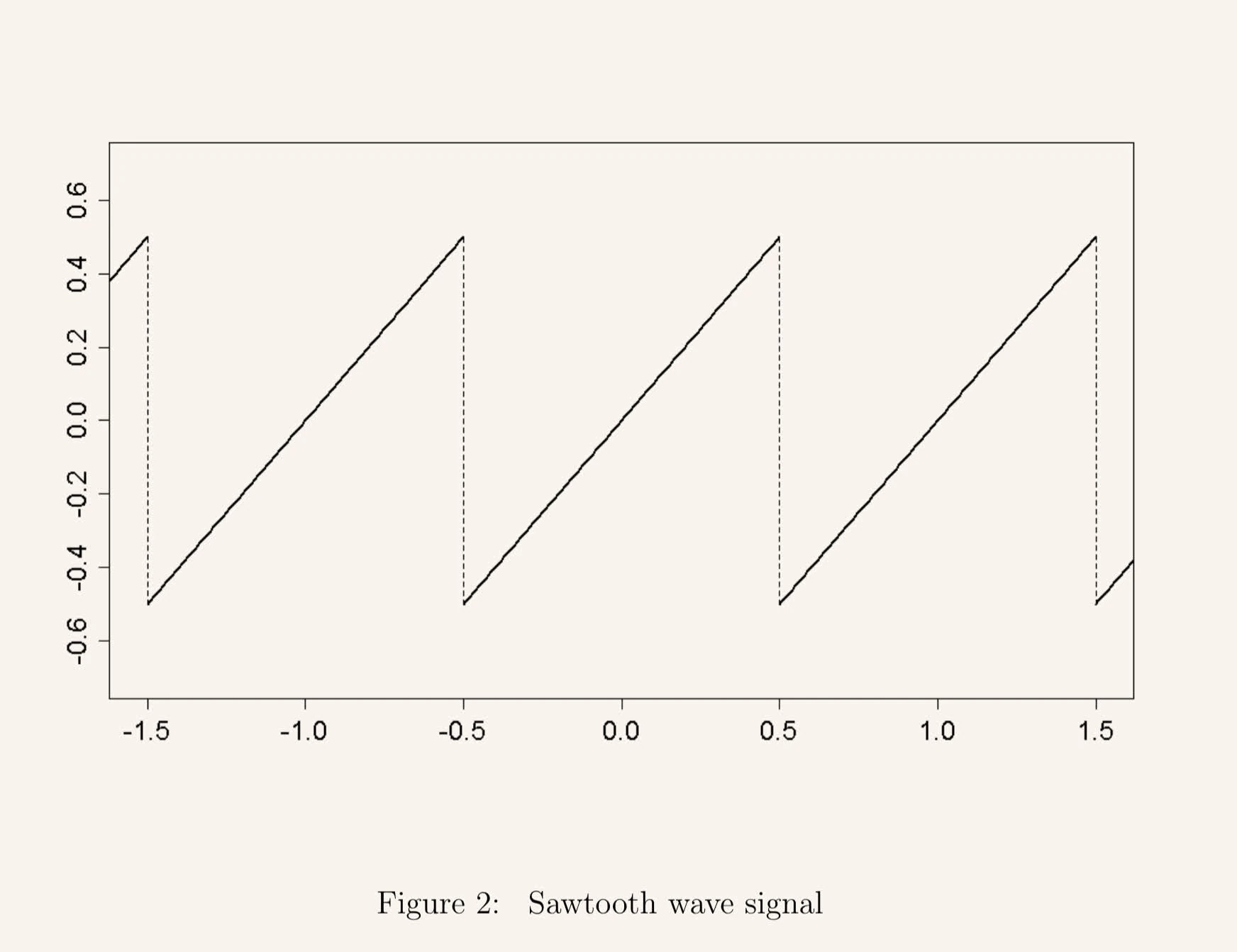
Sawtooth wave

A sawtooth wave function is defined as:

$$f(t) = \frac{2A}{T}(t - \frac{T}{2})$$

import sympy as sp
 
t = sp.symbols('t')
T = 1
A = 0.5
 
f_t = 2 * A / T * (t - T/2)
 
RMS = sp.sqrt(1/T * sp.integrate(f_t**2, (t, 0, T)))

RMS = $\frac{\sqrt{3}}{6}$

1.c

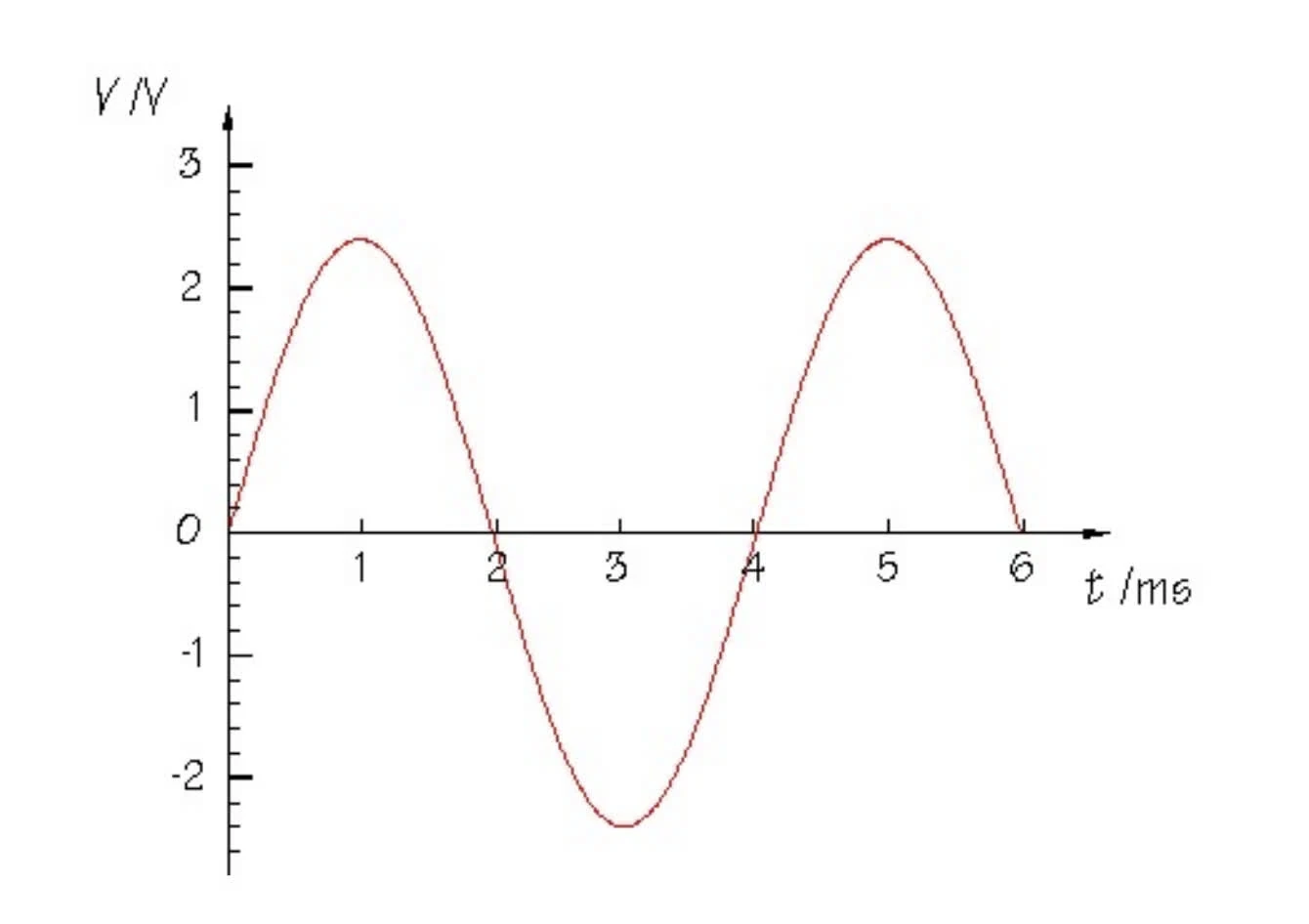
sine wave

A general form of the sine wave can be written as

$$f(t) = A \sin(\omega t + \phi)$$

Amplitude is 2.3, no phase shift

RMS = $\frac{2.3}{\sqrt{2}}$

---

problème 2.

Find the cutoff frequency of the following low-pass filters.

Cutoff frequency of low-pass filters, the frequency at which the amplitude falls to $\frac{1}{\sqrt{2}} \approx 0.707$

2.a

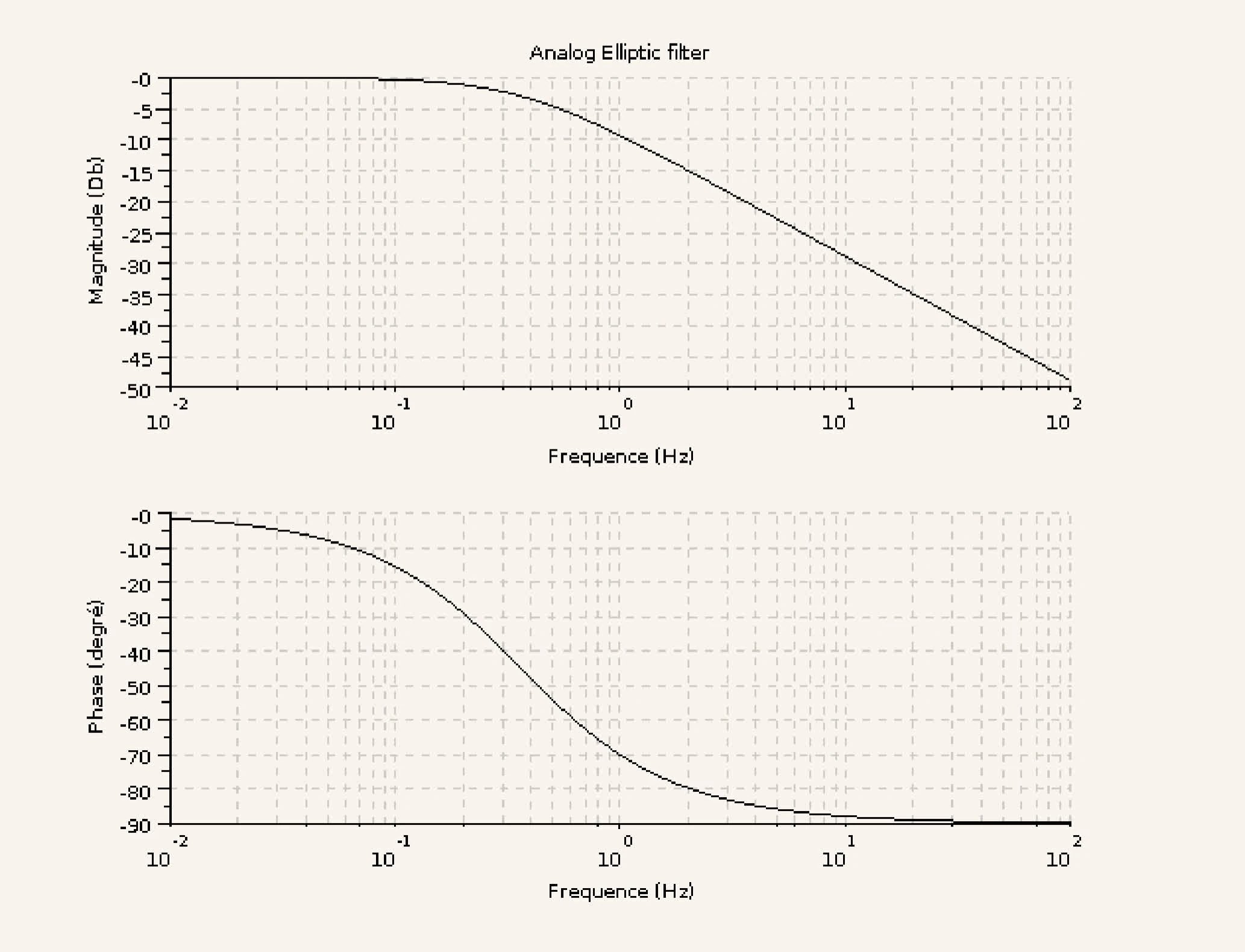
0.05Hz

2.b

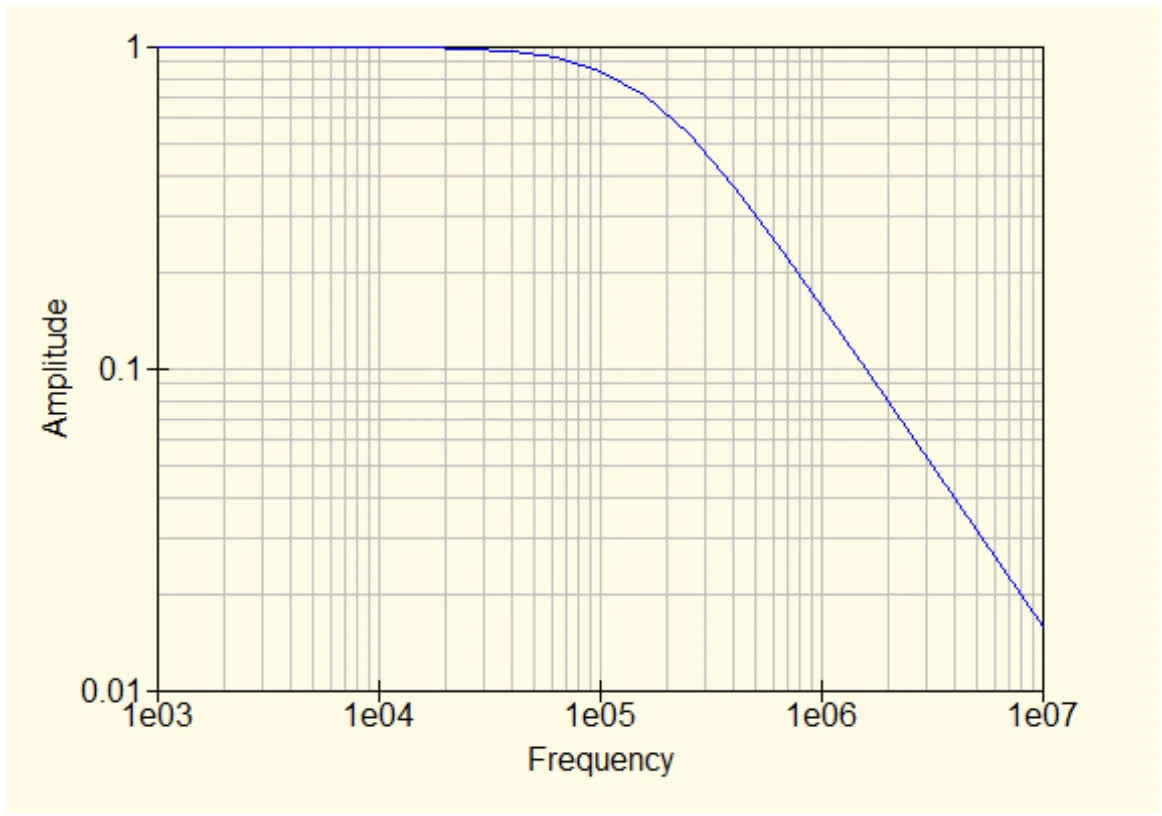
approx. 1.1e05 Hz

2.c

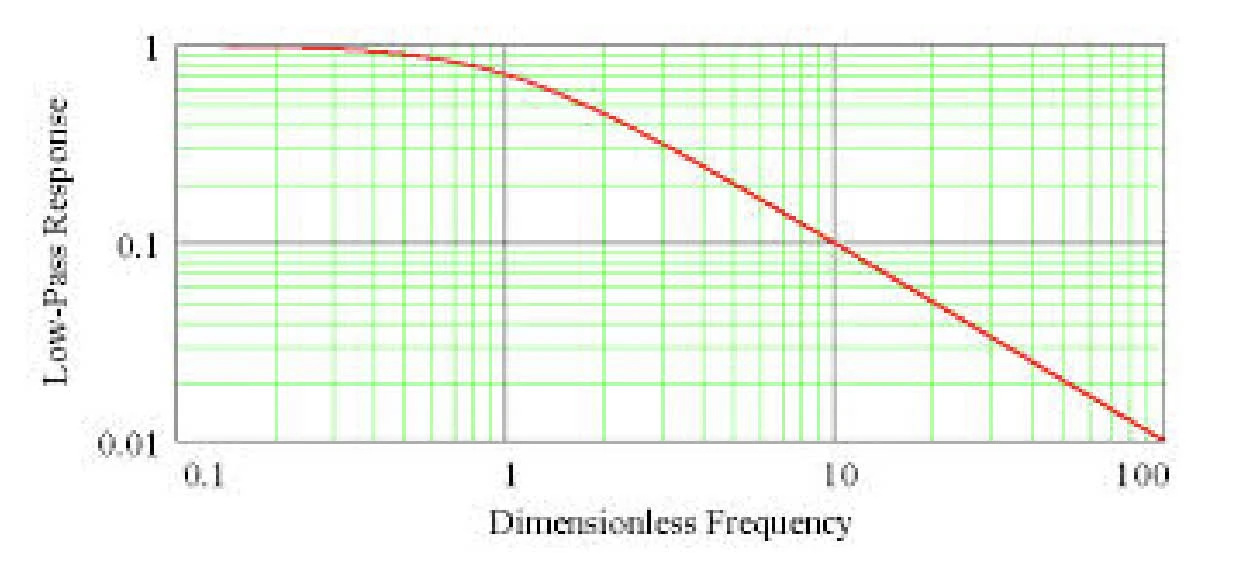
approx 1.1Hz