---
date: '2025-01-18'
description: and mathematical framework of transformers
id: induction heads
modified: 2026-06-05 15:08:29 GMT-04:00
seealso:
  - '[[thoughts/Transformers|Transformers]]'
  - '[[thoughts/LLMs|LLMs]]'
tags:
  - interp
  - ml
title: induction heads
transclude:
  title: false
created: '2025-01-18'
published: '2025-01-18'
pageLayout: default
slug: thoughts/induction-heads
permalink: https://aarnphm.xyz/thoughts/induction-heads.md
generator:
  quartz: v4.6.0
  hostedProvider: Cloudflare
  baseUrl: aarnphm.xyz
full: https://aarnphm.xyz/llms-full.txt
---
@elhage2021mathematical, @olsson2022context

## virtual weights

```jsx imports={Zoomable,VirtualWeights}
<Zoomable label="virtual weights diagram">
  <VirtualWeights caption="Note that the high linearity of the network is very much specific to Transformers; even ResNets, with non-linear activation functions between layers, do not factor this cleanly." />
</Zoomable>
```

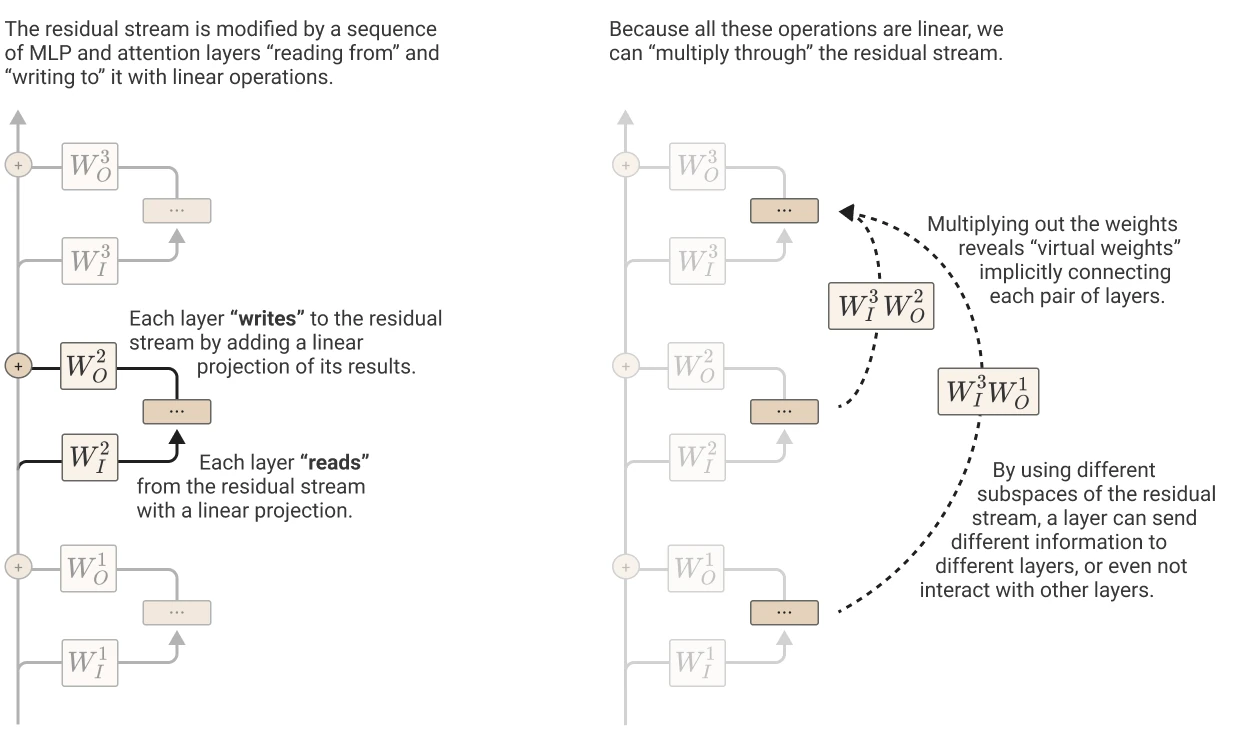
<p data-codeblock="sms" class="text">Each layer performing an arbitrary linear transformations to "read in" information, and performs another arbitrary linear transformers to "write out" back to the residual stream.</p>

In a sense, they don’t have [[thoughts/induction heads#privileged basis]]

One salient property of linear residual stream is that we can think of each explicit pairing as “virtual weights” [^attention]. These virtual weights are the product of the output weights of one layer with the input weights of another (ie. $W^2_{I}W_{O}^1$), and describe the extent to which a later layer reads in the information written by a previous layer.

[^attention]: Note that for attention layers, there are three different kinds of input weights:$W_{Q}, W_{K}, W_{V}$. For simplicity and generality, we think of layers as just having input and output weights here.

## privileged basis

see also: <https://transformer-circuits.pub/2023/privileged-basis/index.html>

tldr: we can rotate it all matrices interacting with the layers without modifying the models’ behaviour.