--- date: '2024-12-13' description: for relational database id: Design theory modified: 2026-06-05 15:08:42 GMT-04:00 tags: - sfwr3db3 title: Design theory created: '2024-12-13' published: '2024-12-13' pageLayout: default slug: thoughts/university/twenty-four-twenty-five/sfwr-3db3/Design-theory permalink: https://aarnphm.xyz/thoughts/university/twenty-four-twenty-five/sfwr-3db3/Design-theory.md generator: quartz: v4.6.0 hostedProvider: Cloudflare baseUrl: aarnphm.xyz full: https://aarnphm.xyz/llms-full.txt --- > \[!abstract\] Keys > > $K$ is a key if $K$ uniquely determines all of $R$ and no subset of $K$ does > > K is a _superkey_ for relation $R$ if $K$ contains a key of $R$ _see also: [[thoughts/university/twenty-four-twenty-five/sfwr-3db3/Keys and Foreign Keys|keys]]_ ## functional dependency Think of it as ”$X \to Y$ holds in $R$” convention: no braces used for set of attributes, just $ABC$ instead of $\{A,B,C\}$ > \[!note\] properties > > - splitting/combining > - trival FDs > - Armstrong’s Axioms > \[!abstract\] FD are generalisation of keys > > superkey: $X \to R$, must include all the attributes of the relation on RHS ### trivial $$ \begin{aligned} A &\to A \\ AB &\to A \\ ABC &\to AD \coloneqq ABC \to D \end{aligned} $$ always hold (right side is a subset) ### splitting/combining right side of FDs $$ X \to A_{1} A_{2} \ldots A_{n} \text{ holds for R } $$ when each of $X \to A_{1}$, $X \to A_{2}$, …, $X \to A_{n}$ _holds for_ $R$ ex: $A \to BC$ is equiv to $A \to B$ and $A \to C$ ex: $A \to F$ and $A \to G$ can be written as $A \to FG$ ### Armstrong’s Axioms Given $X,Y,Z$ are sets of attributes #### rules | Rule | Description | | ------------- | ------------------------------------------- | | Reflexivity | If $Y \subseteq X$, then $X \to Y$ | | Augmentation | If $X \to Y$, then $XZ \to YZ$ for any $Z$ | | Transitivity | If $X \to Y$ and $Y \to Z$, then $X \to Z$ | | Union | If $X \to Y$ and $X \to Z$, then $X \to YZ$ | | Decomposition | If $X \to YZ$, then $X \to Y$ and $X \to Z$ | #### dependency inference $A \to C$ is _implied_ by $\{A \to B, B \to C\}$ #### transitivity example: Key List all the keys of $R(A,B,C,D)$ with the following FDs: - $B \to C$ - $B \to D$ sol: $$ \begin{aligned} B \to C &\text{ and } B \to D &(\text{given})\\ B &\to CD &(\text{Union})\\ AB &\to ACD &(\text{Augmentation})\\ AB &\to ABCD &(\text{Reflexivity and Union})\\ \end{aligned} $$ #### closure test Given attribute set $Y$ and FD set $F$, we have $Y_F^{+}$ is the closure of $Y$ _relative_ to $F$ > Or set of all FDs given/implied by $Y$ _Steps_: - Start: $Y_F^{+}=Y, F^{'}=F$ - While there exists a $f \in F^{'}$ s.t $\text{LHS}(F) \subseteq Y_F^{+}$: - $Y_F^{+} = Y_F^{+} \cup \text{RHS}(f)$ - $F^{'} = F^{'} - f$ - End: $Y \to B \forall B \in Y_F^{+}$ #### minimal basis The idea is to remove redundant FDs. > \[!tip\] for minimal cover for FDs > > - Right sides are **single** attributes > - No FDs can be removed, otherwise $F^{'}$ is no longer a minimal basis > - No attribute can be removed from a **LEFT SIDE** construction: 1. decompose RHS to single attributes 2. repeatedly try to remove a FD to see if the remaining FDs are equivalent to the original set - or $\forall f in F^{'} \mid \text{test whether } J=(F^{'}-f)^{+}$ is equivalent to $F^{+}$ 3. repeatedly try to remove an attribute from LHS to see if the removed attribute can be derived from the remaining FDs. ## Schema decomposition goal: avoid redundancy and minimize anomalies (update and deletion) w/o losing information > One can also think of projecting FDs as [[thoughts/geometric projections]] within a given FDs space > \[!note\] good properties to have > > - lossless join decomposition (should be able to reconstruct after decomposed) > - avoid anomalies (redundant data) > - preservation: $(F_{1} \cup F_{2} \cup \ldots \cup F_n)^{+} = F^{+}$ > \[!note\]- information loss with decomposition > > - Decompose $R$ into $S$ and $T$ > - consider FD $A \to B$ with $A \in S$ and $B \in T$ > - FD loss > - Attribute $A$ and $B$ not in the same relation (thus must join $T$ and $S$ to enforce $A \to B$, which is expensive) > - Join loss > - neither $(S \cap T) \to S$ nor $(S \cap T) \to T$ is in $F^{+}$ > A lossy decomposition results in the reconstruction of components to include additional information that is not in the original constructions > \[!question\] how can we test for losslessness? > > A binary decomposition of $R=(R,F)$ into $R_{1}=(R_{1},F_{1})$ and $R_{2}=(R_{2},F_{2})$ is _lossless_ iff: > > 1. $(R_{1} \cap R_{2}) \to R_{1}$ is the $F^{+}$ > 2. $(R_{1} \cap R_{2}) \to R_{2}$ is the $F^{+}$ if $R_{1} \cap R_{2}$ form a superkey of either $R_{1}$ or $R_{2}$, then decomposition of $R$ is lossless ### Projection - Starts with $F_i = \emptyset$ - For each subset $X \text{ of } R_i$ - Compute $X^{+}$ - For each attribute $A \in X^{+}$ - If $A$ in $R_i$: add $X \to A$ to $F_i$ - Compute minimal basis of $F_i$ ## Normal forms $$ \text{BCNF} \subseteq 3\text{NF} \subseteq 2\text{NF} \subseteq 1\text{NF} $$ | Normal Form | Definition | Key Requirements | Example of Violation | How to Fix | | ----------------------------- | ---------------------------------------------------------------------------------- | ------------------------------------------------------------------------------------------------------------------------------ | ----------------------------------------------------------------------------------------------------------------------------------------- | ------------------------------------------------------------------------------------------------- | | First Normal Form (1NF) | All columns contain atomic values and there are no repeating groups. | - Each cell holds a single value (atomicity)
- No repeating groups or arrays | A column storing multiple phone numbers in a single cell (e.g., “123-4567, 234-5678”). | Split the values into separate rows or columns so each cell is atomic. | | Second Normal Form (2NF) | A 1NF table where every non-key attribute depends on the whole of a composite key. | - Already in 1NF
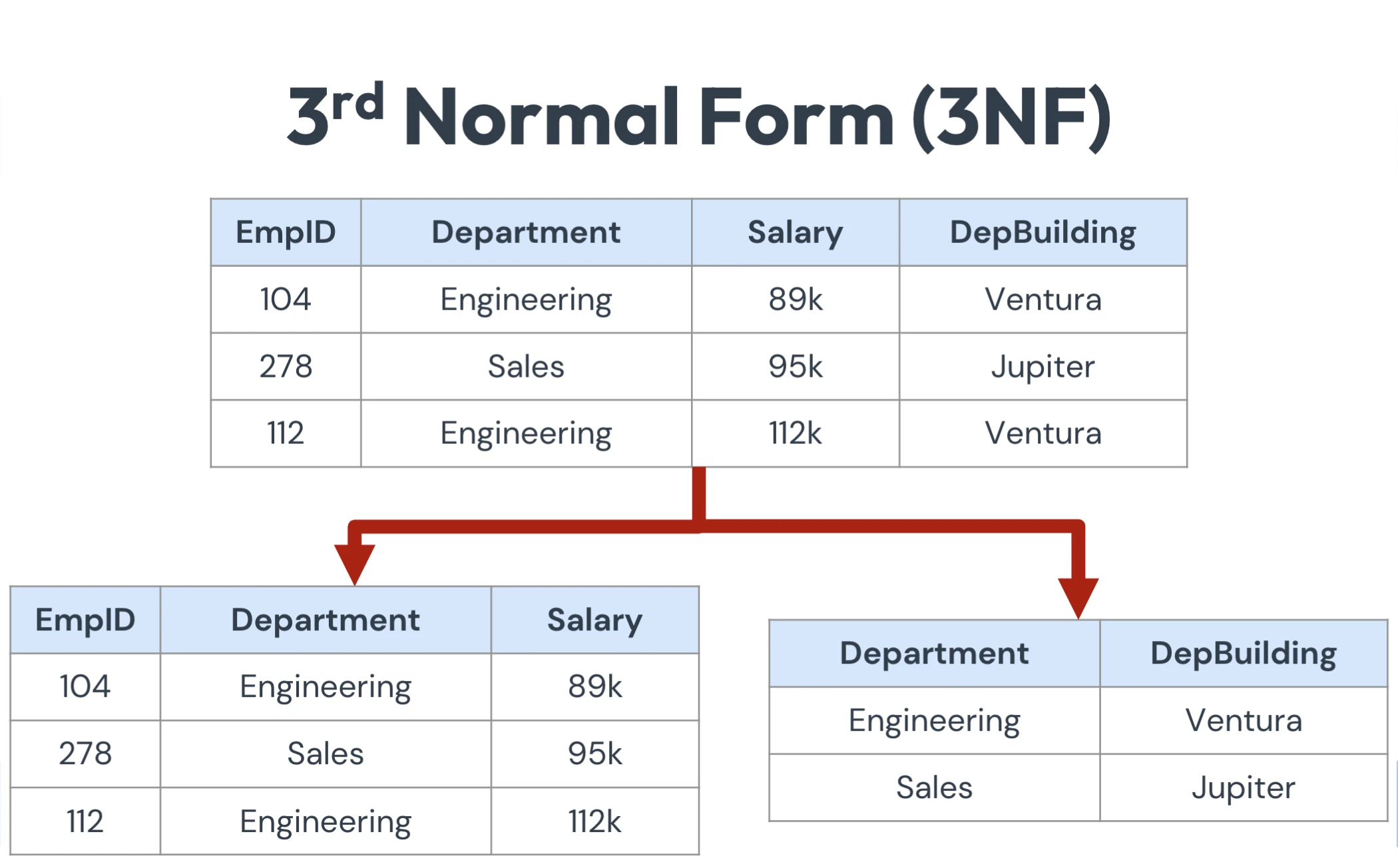
- No partial dependencies on a composite primary key | A table with a composite primary key (e.g., StudentID, CourseID) where a non-key attribute (e.g., StudentName) depends only on StudentID. | Move attributes that depend on only part of the key into a separate table. | | Third Normal Form (3NF) | A 2NF table with no transitive dependencies. | - Already in 2NF
- No transitive dependencies (non-key attributes depend only on the key, not on other non-key attributes) | A table where AdvisorOffice depends on AdvisorName, which in turn depends on StudentID. | Put attributes like AdvisorName and AdvisorOffice in a separate Advisor table keyed by AdvisorID. | | Boyce-Codd Normal Form (BCNF) | A stronger version of 3NF where every determinant is a candidate key. | - For every functional dependency X → Y, X must be a candidate key | A table where Professor → Course but Professor is not a candidate key. | Decompose the table so that every functional dependency has a candidate key as its determinant. | ### 1NF > no multi-valued attributes allowed idea: think of storing a list of a values in an attributes counter: `Course(name, instructor, [student, email]*)` ### 2NF > non-key attributes depend on candidate keys idea: consider non-key attribute $A$, then there exists an FD $X$ s.t. 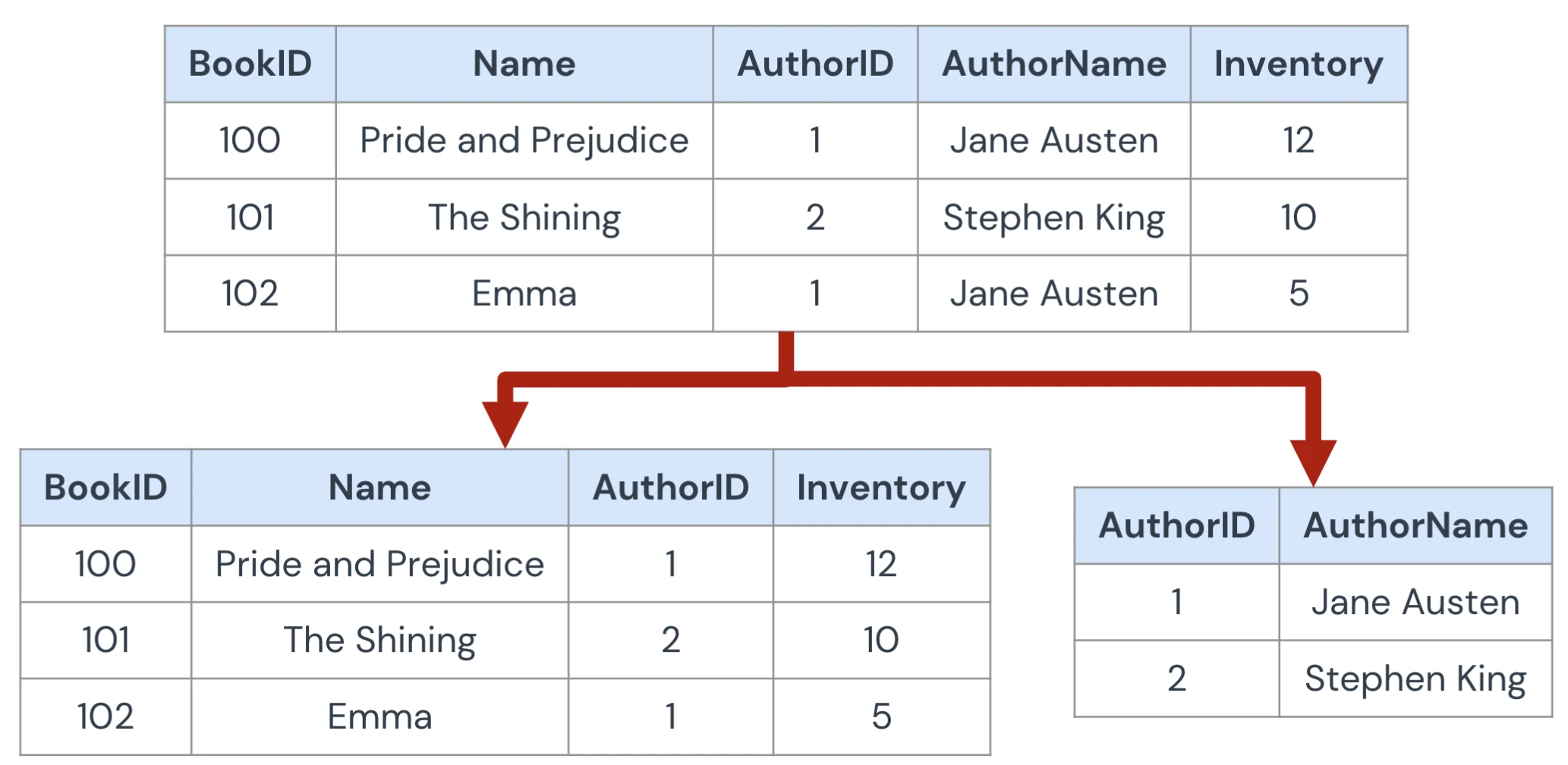$X \to A$ and $X$ is a _candidate key_ ![[thoughts/university/twenty-four-twenty-five/sfwr-3db3/second-normal-form.webp|Second normal form, hwere AuthorName is dependent on AuthorID]] ### 3NF > non-prime attribute depend _only_ on candidate keys idea: consider FD $X \to A$, then either $X$ is a superkey, or $A$ is prime (part of a key) counter: $\text{studio} \to \text{studioAddr}$, where `studioAddr` depends on `studio` which is not a candidate key
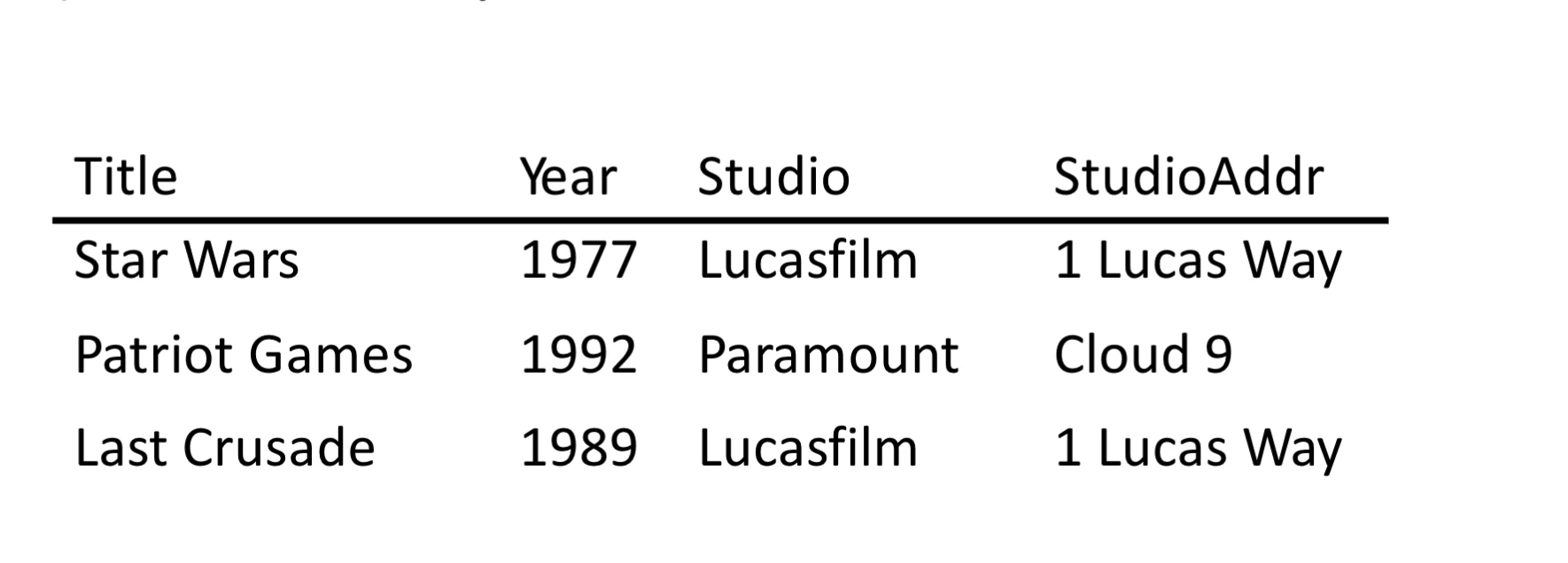
Three normal form counter example
> \[!theorem\] Theorem 1. > > It is always possible to convert a schema to lossless join, dependency-preserving 3NF > \[!tip\] what you get from 3NF > > - Lossless join > - dependency preservation > - anomalies (doesn’t guarantee) ### Boyce-Codd normal form (BCNF) > on additional restriction over 3NF where all non-trivial FDs have superkey LHS > \[!theorem\] Theorem 2. > > We say a relation $R$ is in BCNF if $X \to A$ is a non-trivial FD that holds in $R$, and $X$ is a superkey [^nontrivial] [^nontrivial]: means $A$ is not contained in $X$ > \[!tip\] what you get from BCNF > > - no dependency preservation (all original FDs should be satisfied) > - no anomalies > - Lossless join #### decomposition into BCNF relation $R$ with FDs $F$, look for a BCNF violation $X \to Y$ ($X$ is not a superkey) - Compute $X^{+}$ - find $X^{+} \neq X \neq \text{ all attributes }$ ($X$ is a superkey) - Replace $R$ by relations with - $R_{1} = X^{+}$ - $R_{2} = R - (X^{+} - X) = R - X^{+} \cup X$ - Continue to recursively decompose the two new relations - _Project_ given FDs $F$ onto the two new relations.