PID Controller from input signals
Transfer function for angular speed:
1+τsA
The input signal that begins at time t0 and its minimum and maximum values are given by umin,umax.
The resulting output signal is initially at y0 and eventually settles down for a steady state value of yss.
The steady state gain A is given by:
A=umax−uminyss−y0=△u△y
Time constant τ is time required for output to increase from initial value to 0.632×△y
Let t1 is time when change in output is 0.632×△y:
y(t1)τ=0.632×(yss−y0)+y0=t1−t0
find the transfer function
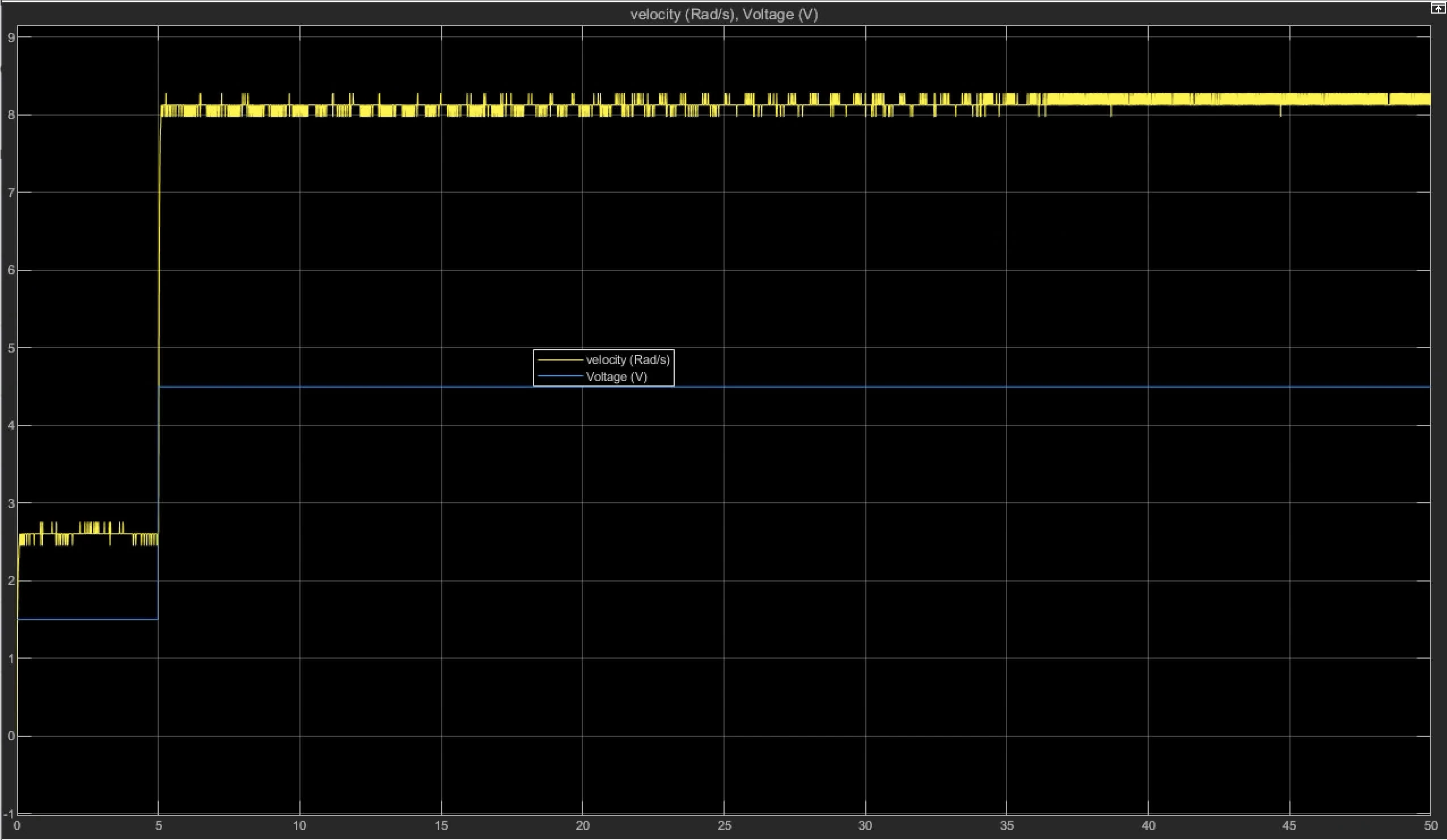 △y△vAtarget velocityτ≈0.029secs=3V=8.285−2.454=5.831rad/s=35.831=1.9436666667rad/s=2.454+0.632∗5.831=6.139192rad/s
△y△vAtarget velocityτ≈0.029secs=3V=8.285−2.454=5.831rad/s=35.831=1.9436666667rad/s=2.454+0.632∗5.831=6.139192rad/s
note: reach it at around 5.029 sec
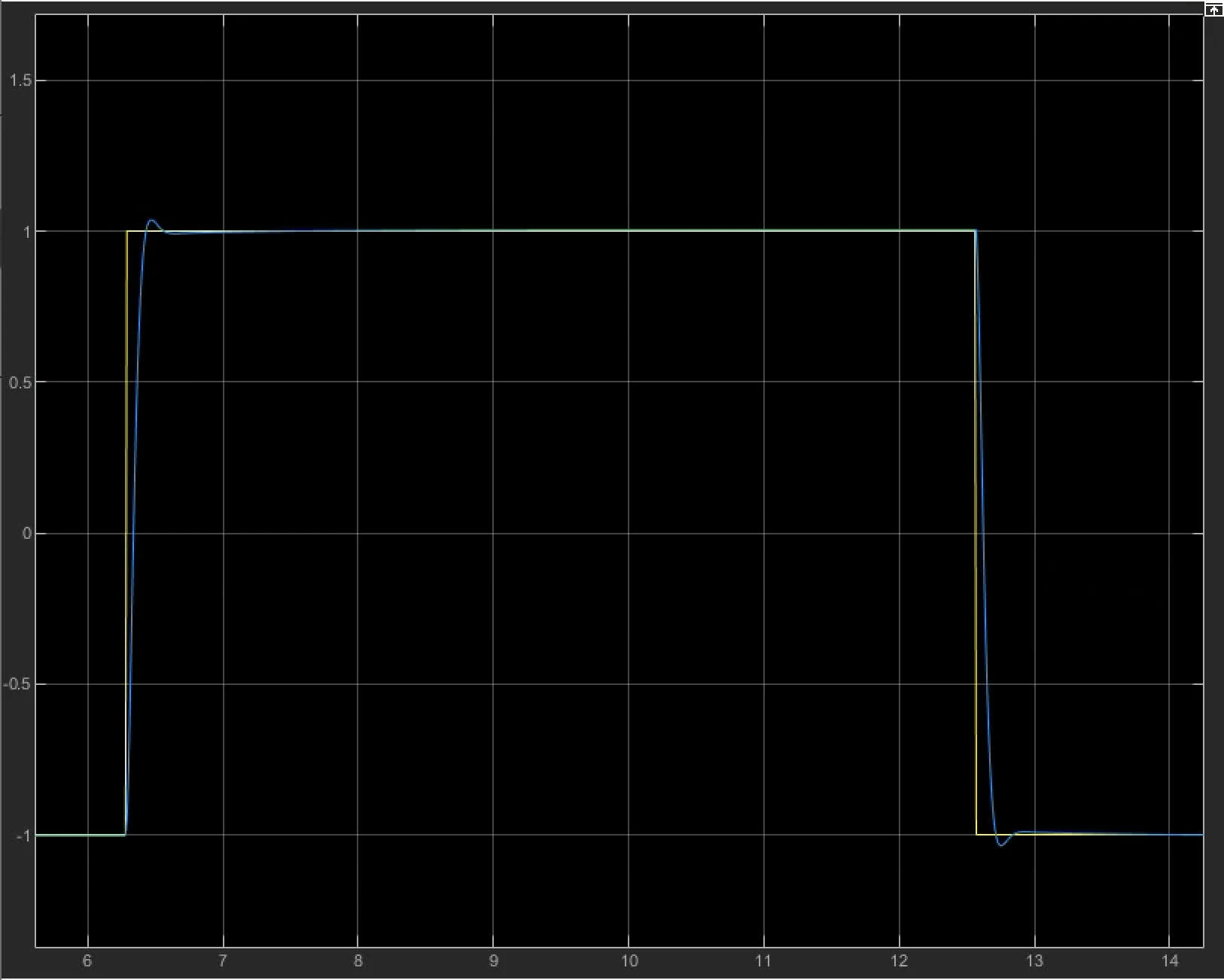
graphs
see simulink file
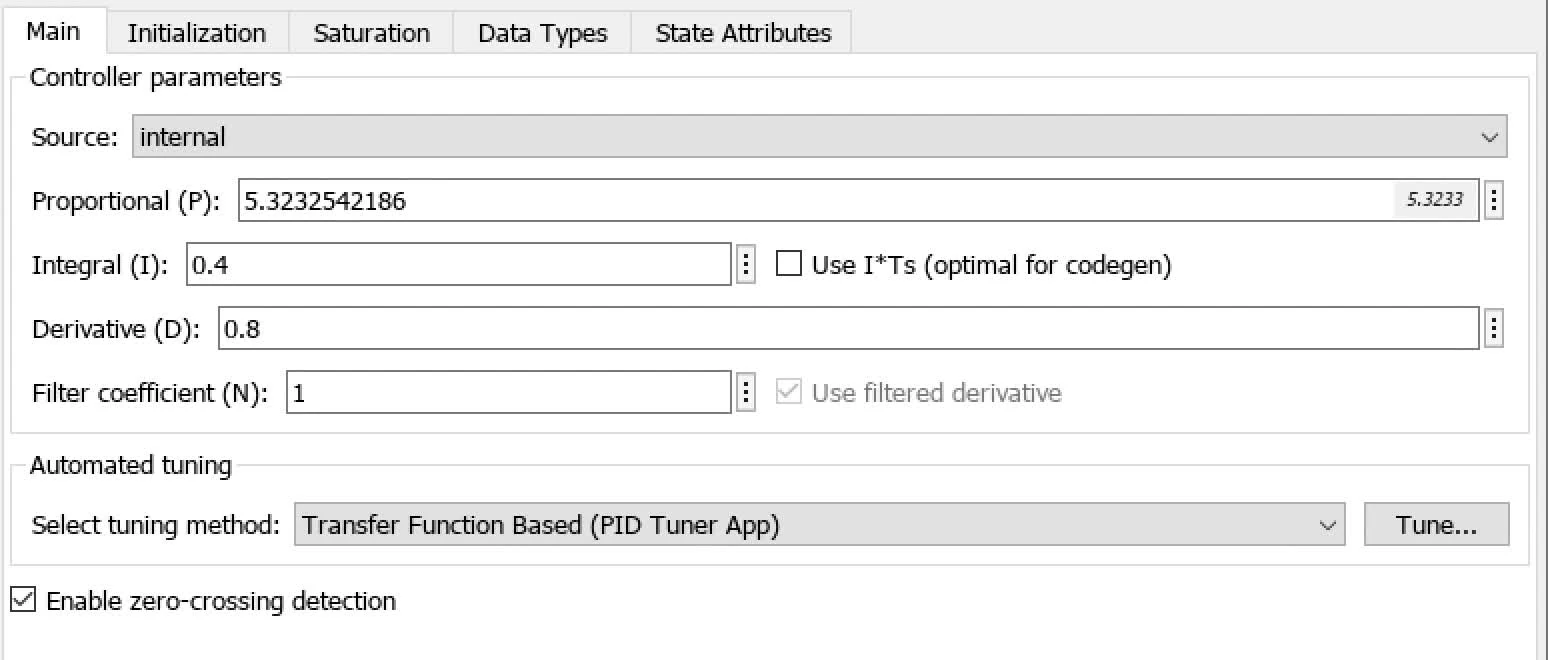 proportional P=350∗180π
proportional P=350∗180π


 proportional
proportional