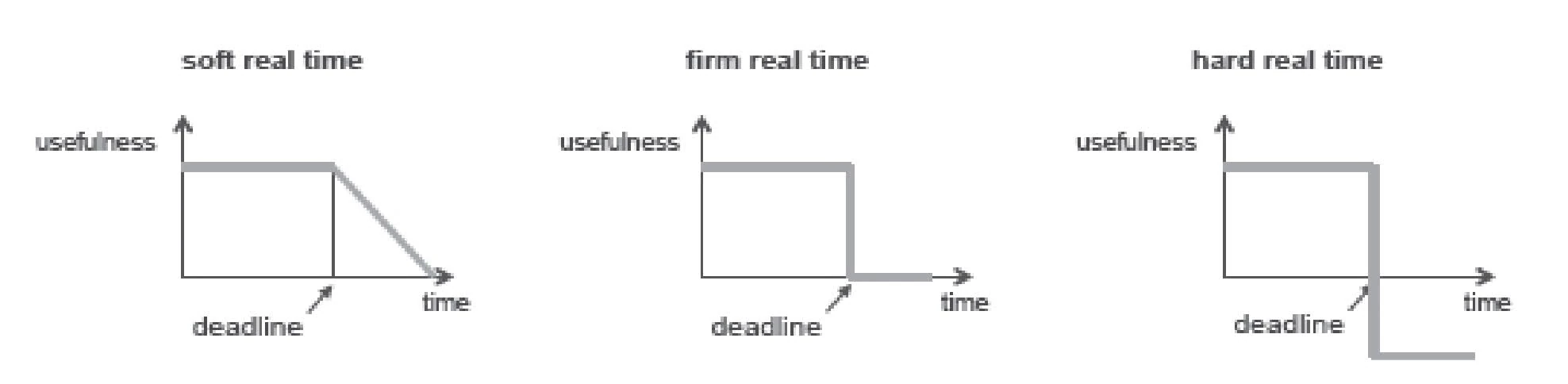
correctness:
drift is RoC of the clock value from perfect clock. Given clock has bounded drift then
Monotonicity:
kernels
syscall in kernel: User space and Kernel Space are in different spaces
graph LR A[procedure] --[parameters]--> B[TRAP] B --> C[Kernel] C --> B --> A
Important
a user process becomes kernel process when execute syscall
Scheduling ensures fairness, min response time, max throughput
| OS | RTOS | |
|---|---|---|
| philos | time-sharing | event-driven |
| requirements | high-throughput | schedulablity (meet all hard deadlines) |
| metrics | fast avg-response | ensureed worst-case response |
| overload | fairness | meet critical deadlines |
Kernel programs can always preempt user-space programs
Kernel program example:
#include <linux/init.h> /* Required by macros*/
#include <linux/kernel.h> /*KERN_INFO needs it*/
#include <linux/module.h>
static char *my_string __initdata = "dummy";
static int my_int __initdata = 4;
/* Init function with user defined name*/
static int __init hello_4_init(void) {
printk(KERN_INFO "Hello %s world, number %d\n", my_string, my_int);
return 0;
}
/* Exit function with user defined name*/
static void __exit hello_4_exit(void) {
printf(KERN_INFO "Goodbye cruel world 4\n");
}
/*Macros to be used after defining init and exit functions*/
module_init(hello_4_init);
module_exit(hello_4_exit)preemption & syscall
The act of temporarily interrupting a currently scheduled task for higher priority tasks.
NOTE:
makedoesn’t recompile if DAG is not changed.
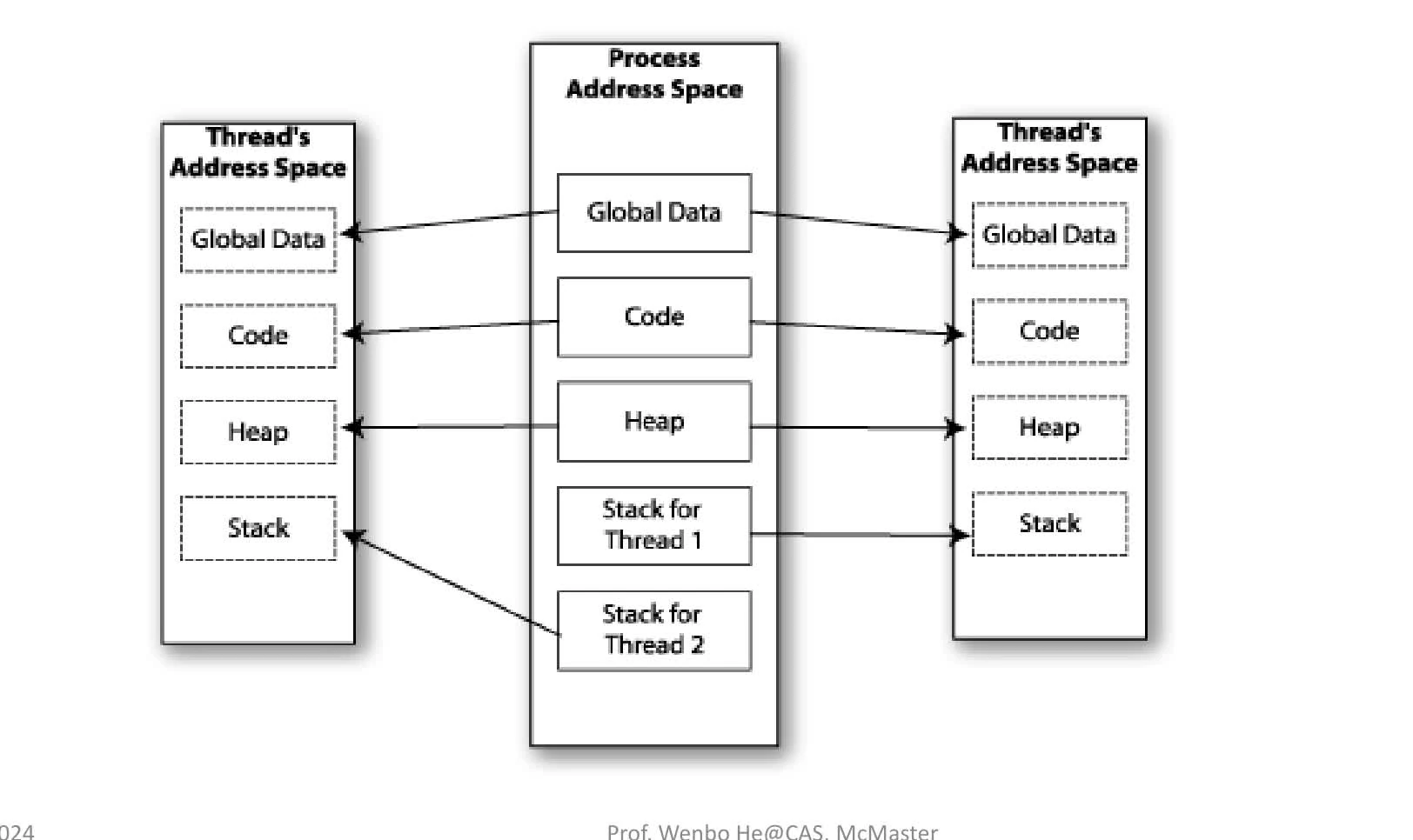
process
- independent execution, logical unit of work scheduled by OS
- in virtual memory:
- Stack: store local variables and function arguments
- Heaps: dyn located (think of
malloc,calloc) - BSS segment: uninit data
- Data segment: init data (global & static variables)
- text: RO region containing program instructions
| stack | heap | |
|---|---|---|
| creation | Member m | Member*m = new Member() |
| lifetime | function runs to completion | delete, free is called |
| grow | fixed | dyn added by OS |
| err | stack overflow | heap fragmentation |
| when | size of memory is known, data size is small | large scale dyn mem |
fork()
- create a
childprocess that is identical to its parents, return0to child process and pid - add a lot of overhead as duplicated. Data space is not shared
variables init b4
fork()will be duplicated in both parent and child.
#include <stdio.h>
int main(int argc, char** argv) {
int child = fork();
int c = 0;
if (child)
c += 5;
else {
child = fork();
c += 5;
if (child) c += 5;
}
printf("%d ", c);
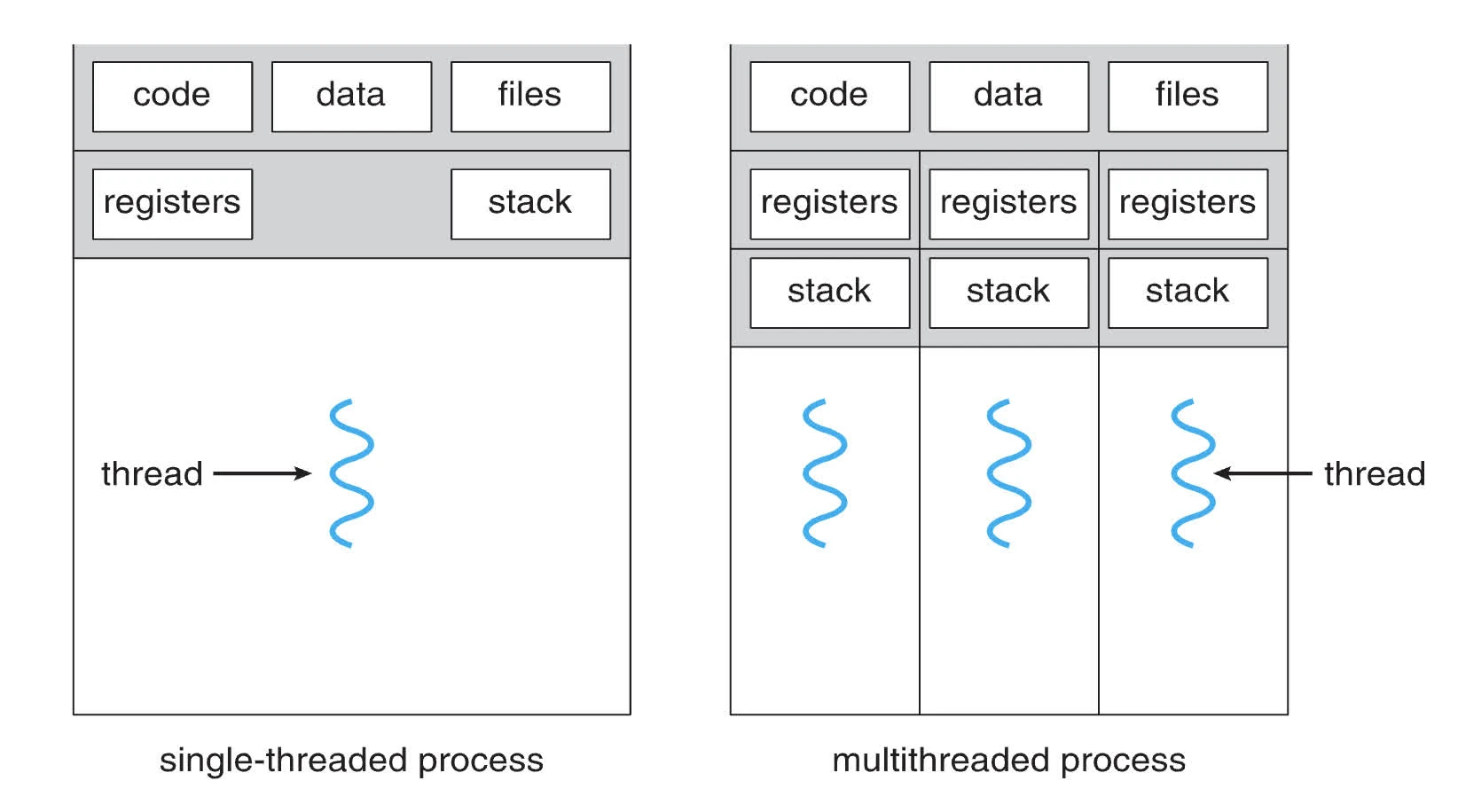
}threads
- program-wide resources: global data & instruction
- execution state of control stream
- shared address space for faster context switching
- Needs synchronisation (global variables are shared between threads)
- lack robustness (one thread can crash the whole program)
#include <pthread.h>
void *foo(void *args) {}
pthread_attr_t attr;
pthread_attr_init(attr);
pthread_t thread;
// pthread_create(&thread, &attr, function, arg);To solve race condition, uses semaphores.
polling and interrupt
-
polling: reading memloc to receive update of an event
-
think of
while (true) { if (event) { process_data() event = 0; } }
-
-
interrupt: receieve interrupt signal
-
think of
signal(SIGNAL, handler) void handler(int sig) { process_data() } int main() { while (1) { do_work() } }
-
| interrupt | polling | |
|---|---|---|
| speed | fast | slow |
| efficiency | good | poor |
| cpu-waste | low | high |
| multitasking | yes | yes |
| complexity | high | low |
| debug | difficult | easy |
process priority
nice: change process priority
- 0-99: RT tasks
- 100-139: Users
lower the NICE value, higher priority
#include <sys/resource.h>
int getpriority(int which, id_t who);
int setpriority(int which, id_t who, int value);set scheduling policy: sched_setscheduler(pid, SCHED_FIFO | SCHED_RR | SCHED_DEADLINE, ¶m)
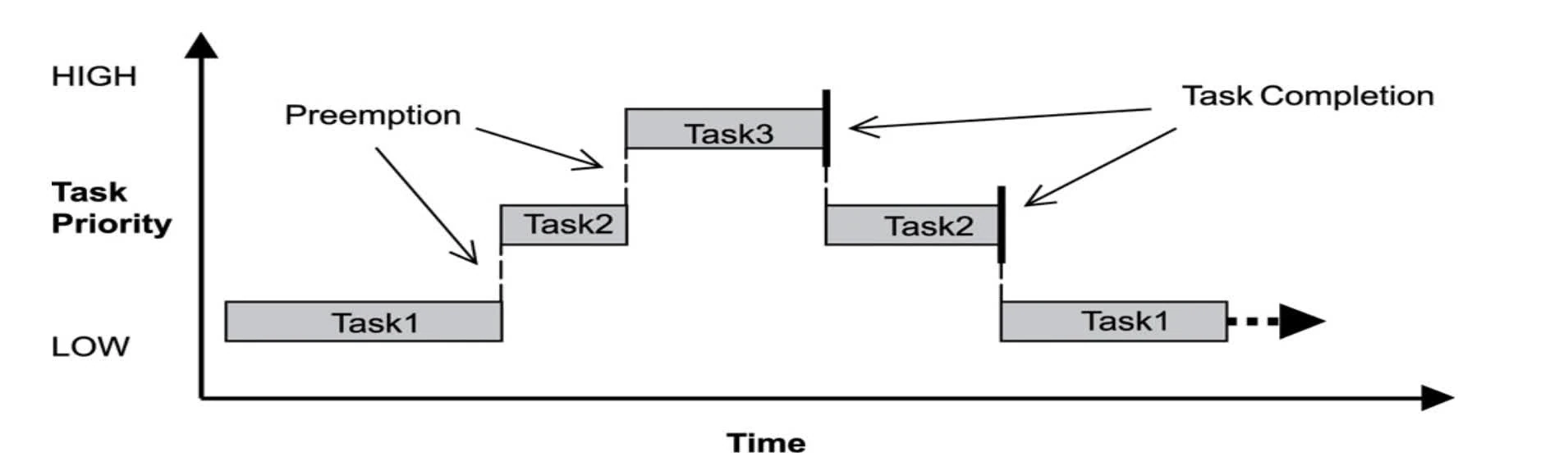
scheduling
- Priority-based preemptive scheduling
Temporal parameters:
Let the following be the scheduling parameters:
| desc | var |
|---|---|
| # of tasks | |
| release/arrival-time | |
| absolute deadline | |
| relative deadline | |
| execution time | |
| response time |
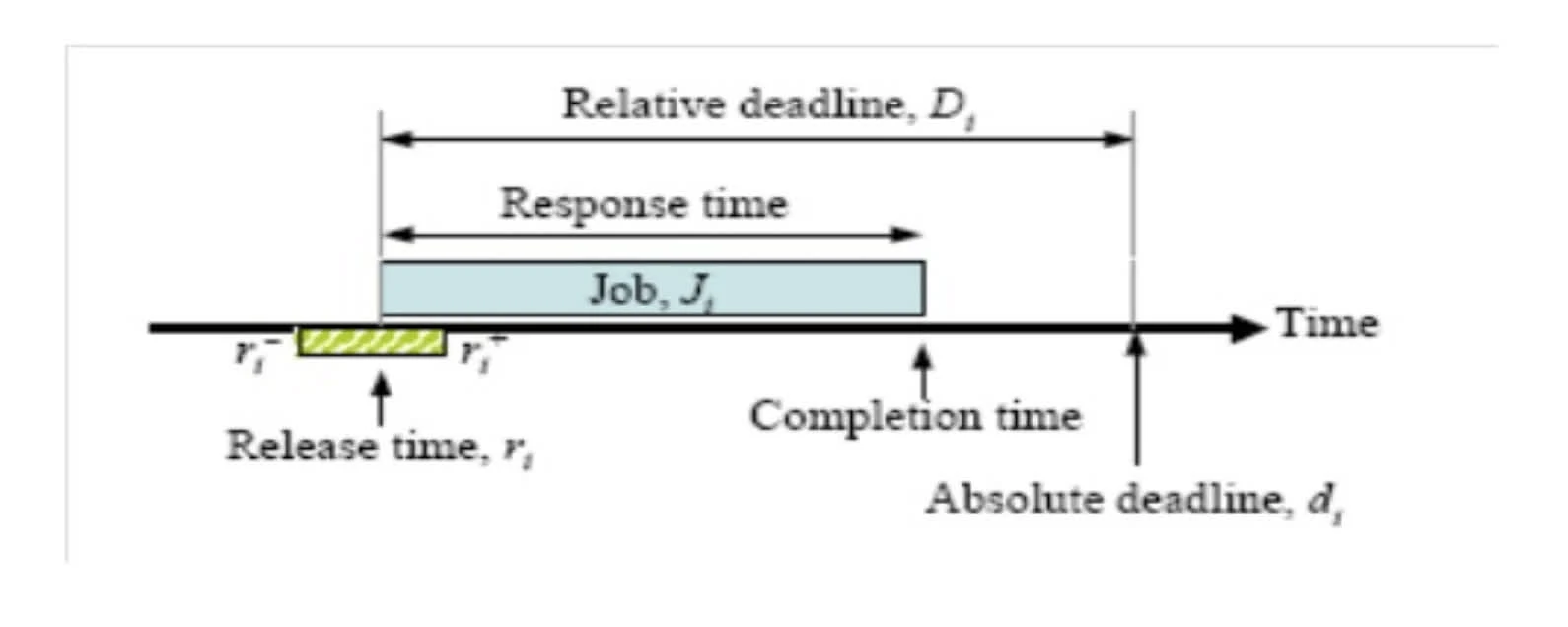
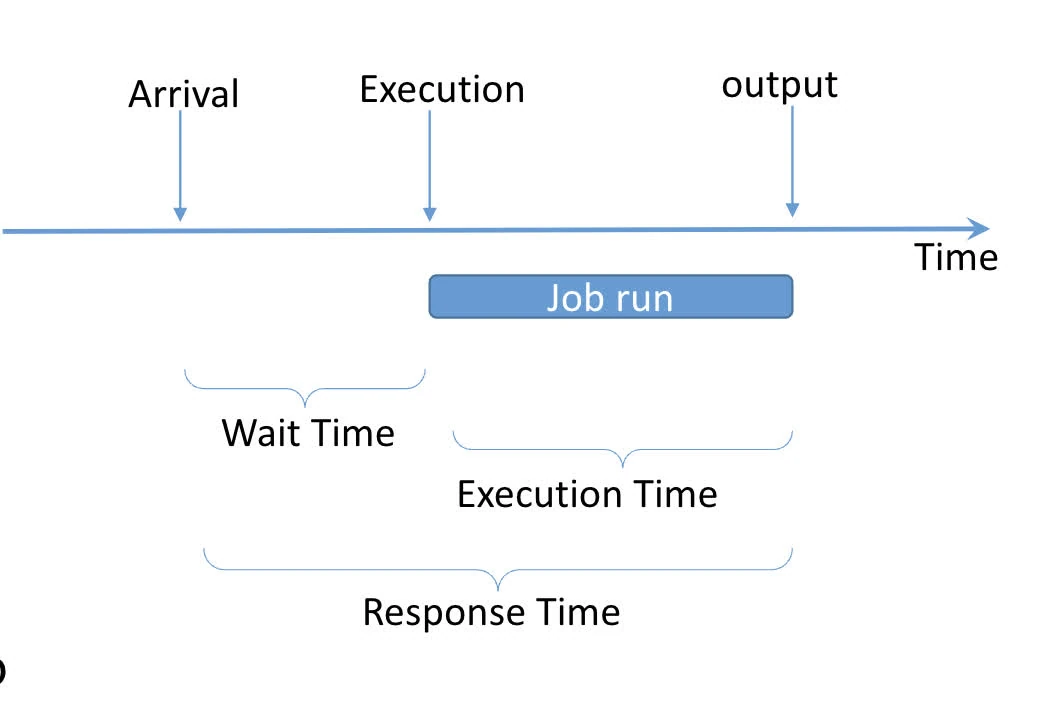
Period of a periodic task is min length of all time intervales between release times of consecutive tasks.
Phase of a Task is the release time of a task , or
in phase are first instances of several tasks that are released simultaneously
Representation
a periodic task can be represented by:
- 4-tuple
- 3-tuple , or
- 2-tuple , or
Utilisation factor
for a task with execution time and period is given by
For system with tasks overall system utilisation is
cyclic executive
assume tasks are non-preemptive, jobs parameters with hard deadlines known.
- no race condition, no deadlock, just function call
- however, very brittle, number of frame can be large, release times of tasks must be fixed
hyperperiod
is the least common multiple (lcm) of the periods.
maximum num of arriving jobs
Frames: each task must fit within a single frame with size ⇒ number of frames
C1: A job must fit in a frame, or for all tasks
C2: hyperperiod has an integer number of frames, or
C3: per task.
task slices
idea: if framesize constraint doesn’t met, then “slice” into smaller sub-tasks
becomes and and
Flow Graph for hyper-period
- Denote all jobs in hyperperiod of frames as
- Vertices:
- job vertices
- frame vertices
- Edges:
- with capacity
- Encode jobs’ compute requirements
- with capacity iff can be scheduled in frame
- encode periods and deadlines
- edge connected job node and frame node if the following are met:
- job arrives before or at the starting time of the frame
- job’s absolute deadline larger or equal to ending time of frame
- with capacity
- encodes limited computational capacity in each frame
- with capacity
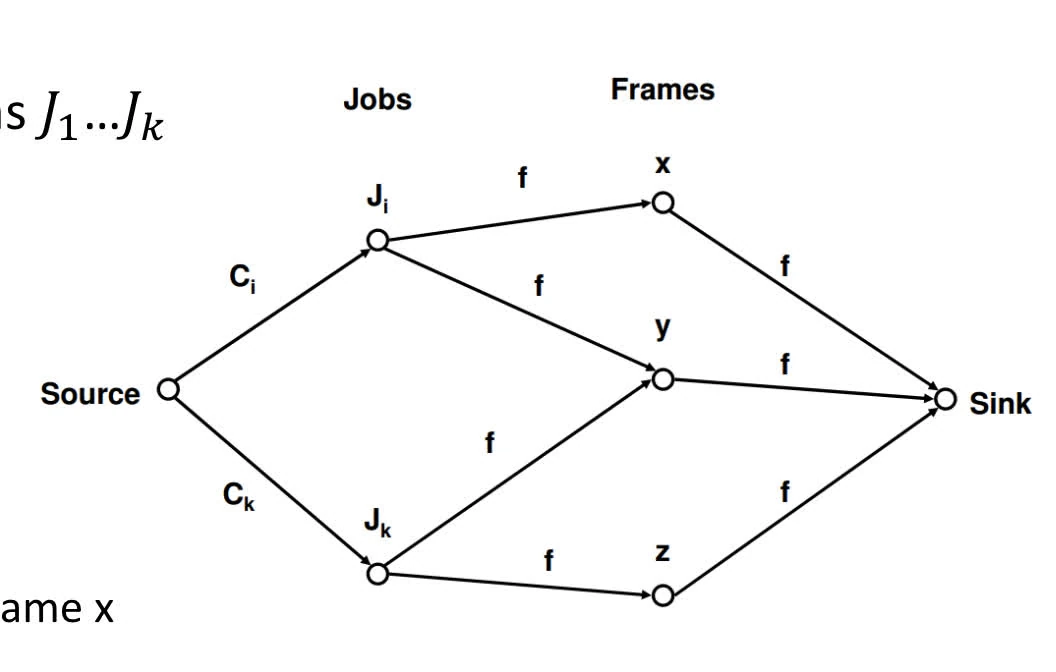
static priority assignment
For higher priority:
- shorter period tasks (rate monotonic RM)
- tasks with shorter relative deadlines (deadline monotonic DM)
rate-monotonic
- running on uniprocessor, tasks are preemptive, no OS overhead for preemption
task has higher priority than task if
schedulability test for RM (Test 1)
Given periodic processes, independent and preemptable, for all processes, periods of all tasks are integer multiples of each other
a sufficient condition for tasks to be scheduled on uniprocessor:
schedulability test for RM (Test 2)
A sufficient but not necessary condition is for periodic tasks
for , we have
schedulability test for RM (Test 3)
Consider a set of task with . Assume all tasks are in phase. to ensure that can be feasibly scheduled, that ( has highest priority given lowest period)
Supposed finishes at . Total number of isntances of task released over time interval is
Thus the following condition must be met for every instance of task released during tim interval :
idea: find such that time and for task 2
general solution for RM-schedulability
The time demand function for task :
holds a time instant chosen as and
deadline-monotonic
- if every task has period equal to relative deadline, same as RM
- arbitrary deadlines then DM performs better than RM
- RM always fails if DM fails
dynamic priority assignment
Priority Inversion
critical sections to avoid race condition
Higher priority task can be blocked by a lower priority task due to resource contention
shows how resource contention can delay completion of higher priority tasks
- access shared resources guarded by Mutex or semaphores
- access non-preemptive subsystems (storage, networks)
Resource Access Control
mutex
serially reusable: a resource cannot be interrupted
If a job wants to use units of resources , it executes a lock , and unlocks once it finished
Non-preemptive Critical Section Protocol (NPCS)
idea: schedule all critical sections non-preemptively
While a task holds a resource it executes at a priority higher than the priorities of all tasks
a higher priority task is blocked only when some lower priority job is in critical section
pros:
- zk about resource requirements of tasks cons:
- task can be blocked by a lower priority task for a long time even without resource conflict
PIP and PCP
Priority Inheritance Protocol (PIP)
idea: increase the priorities only upon resource contention
avoid NPCS drawback
would still run into deadlock (think of RR task resource access)
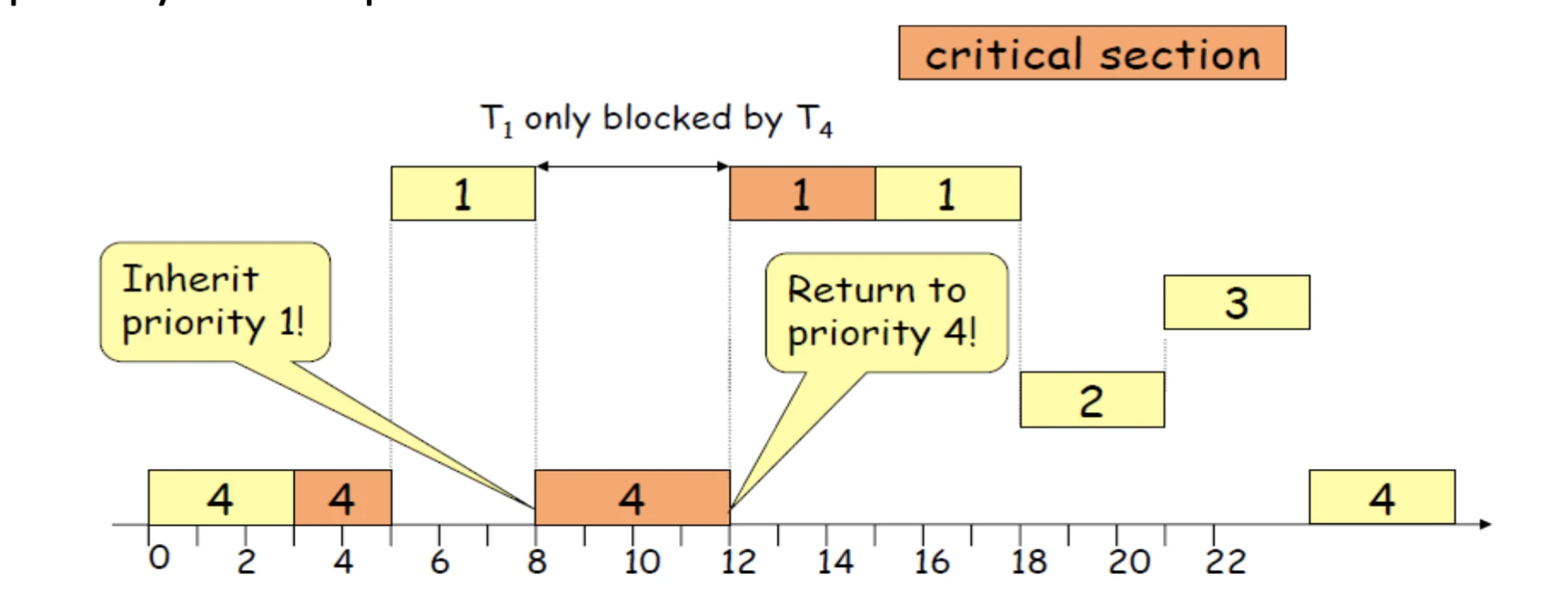
rules:
- When a task T1 is blocked due to non availability of a resource that it needs, the task T2 that holds the resource and consequently blocks T1, and T2 inherits the current priority of task T1.
- T2 executes at the inherited priority until it releases R.
- Upon the release of R, the priority of T2 returns to the priority that it held when it acquired the resource R
Priority Ceiling Protocol (PCP)
idea: extends PIP to prevent deadlocks
- If lower priority task TL blocks a higher priority task TH, priority(TL) ← priority(TH)
- When TL releases a resource, it returns to its normal priority if it doesn’t block any task. Or it returns to the highest priority of the tasks waiting for a resource held by TL
- Transitive
- T1 blocked by T2: priority(T2) ← priority(T1)
- T2 blocked by T3: priority(T3) ← priority(T1)
ceiling(R): highest priority. Each resource has fixed priority ceilingLien vers l'original