SVM and Logistic Regression

See also jupyter notebook

task 1: linear SVM for MNIST classification

part a

Is the implementation of the multi-class linear SVM similar to the end-to-end multi-class SVM that we learned in the class? Are there any significant differences?

Differences	multi-class linear SVM	end-to-end multi-class SVM
Loss function	Uses MultiMarginLoss, which creates a criterion that optimises a multi-class classification hinge loss 1	multi-vector encoding where $h(x) = \arg\max_{y} <w, \Psi(x,y)>$
Architecture	Through a single linear layers based on given input_size and num_classes	optimized over pairs of class scores with multi-vector encoding
Parameter Learning	Uses SGD with minibatches to optimize MML	Whereas we show a theoretical formulation of optimizing over multi-vector encoded space 2

part B

1. Compute the accuracy on the train and test set after each epoch in the training. Plot these accuracies as a function of the epoch number and include it in the report (include only the plot in your report, not all the 2*100 numbers).
2. Compute the hinge loss on the train and test set after each epoch in the training. Plot these loss values as a function of the epoch number and include it in the report.(include only the plot in your report, not all the 2*100 numbers)
3. Report the last epoch results (including loss values and accuracies) for both train and test sets.
4. Does the model shows significant overfitting? Or do you think there might be other factors that are more significant in the mediocre performance of the model?

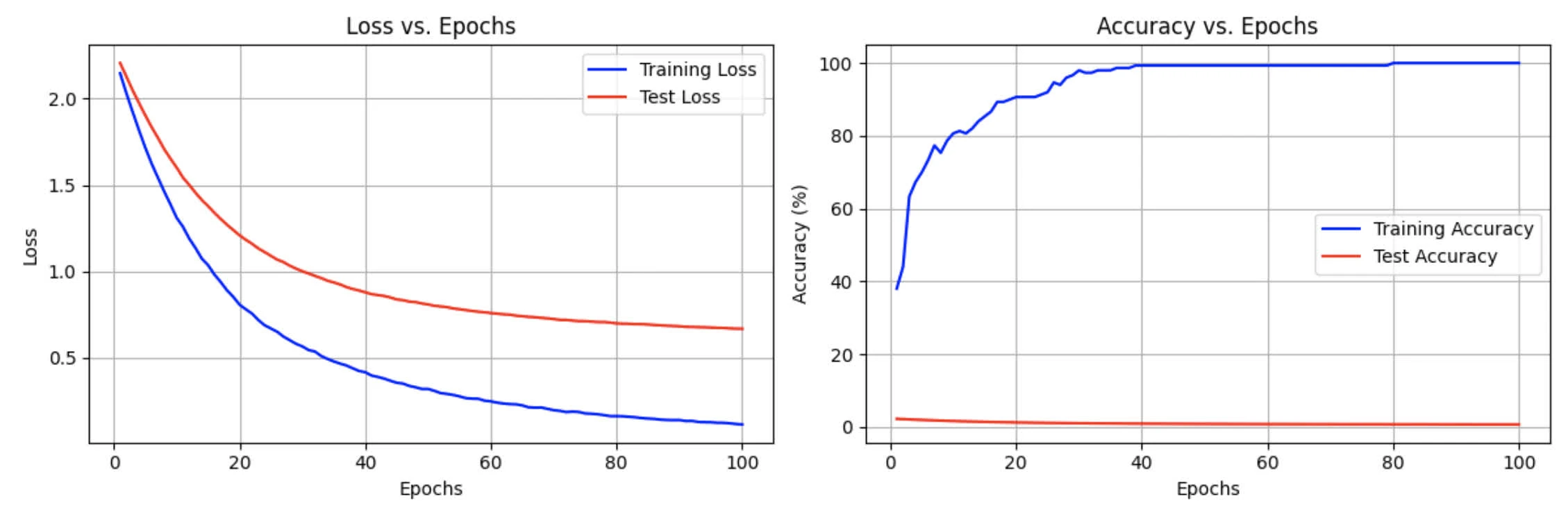
The following includes graph for both accuracy and loss on train/test sets after 100 epochs

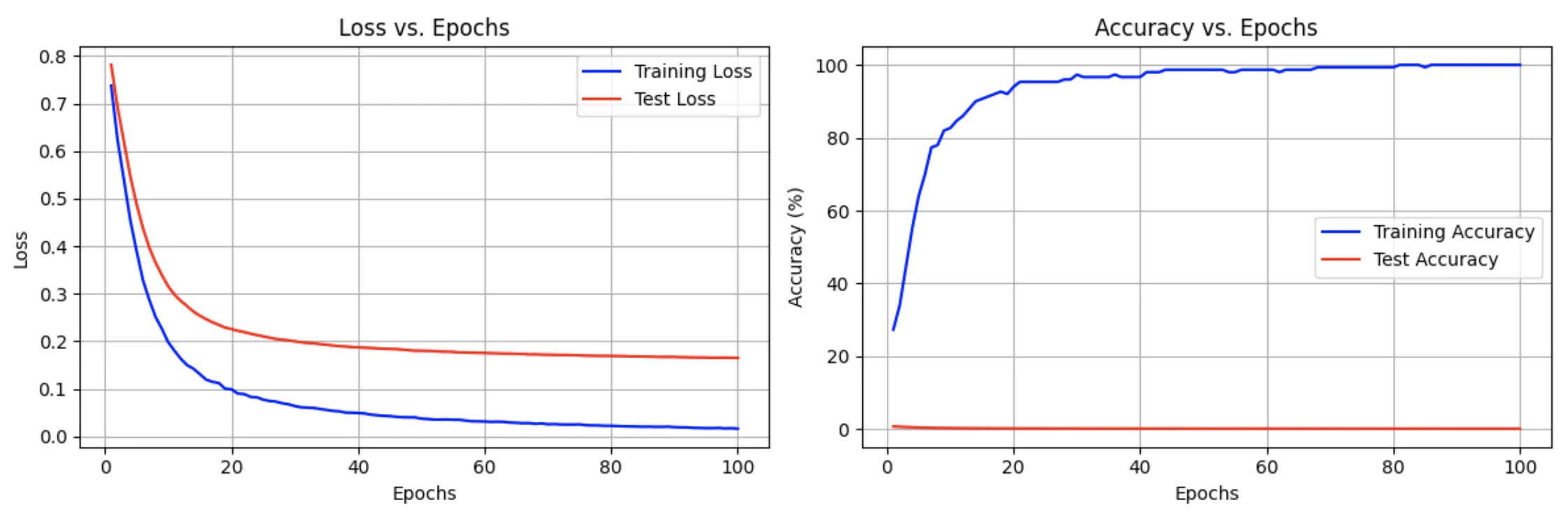
Last epoch results for both train and test sets:

-------------------------------------------------------------
Epoch 100 - Train loss: 0.016170, Train accuracy: 100.00%
         - Test loss: 0.165001, Test accuracy: 78.50%
-------------------------------------------------------------

We observe training accuracy continuing to improve, while test accuracy plateaus. Same observation can be made for in Loss vs. Epochs graph, where gap between training and test loss increases as epochs increase

While this shows evidence of overfitting, one can argue there are factors affecting model performance:

Liminal training data:

• we are currently only use 0.25% of MNIST dataset (which is around 150 samples) ³
• This makes it difficult for the model to learn generalizable patterns

Model limitation:

• Linear SVM can only learn linear decision boundaries
• MNIST datasets requires non-linear decision boundaries to achieve high performance (we observe this through relatively quick plateau test accuracy after 78.5%)

We don’t observe in degrading test performance, which is not primarily behaviour of overfitting.

part c

Weight decay works like regularization. Set weight decay to each of the values (0.1, 1, 10) during defining the SGD optimizer (see SGD optimizer documentation for how to do that).

Plot the train/test losses and accuracies per epoch. Also report the last epoch results (loss and accuracy for both train and test) .

Important

Does weight decay help in this case? Justify the results.

The following are logs for set of weight decay from (0.1, 1, 10)

Training with weight decay = 0.1
=============================================================
Epoch 020 - Train loss: 0.1048, Train accuracy: 94.67%
          - Test loss: 0.2342, Test accuracy: 75.30%
-------------------------------------------------------------
Epoch 040 - Train loss: 0.0638, Train accuracy: 98.00%
          - Test loss: 0.2072, Test accuracy: 78.60%
-------------------------------------------------------------
Epoch 060 - Train loss: 0.0520, Train accuracy: 98.67%
          - Test loss: 0.2034, Test accuracy: 79.10%
-------------------------------------------------------------
Epoch 080 - Train loss: 0.0447, Train accuracy: 99.33%
          - Test loss: 0.2043, Test accuracy: 80.00%
-------------------------------------------------------------
Epoch 100 - Train loss: 0.0422, Train accuracy: 99.33%
          - Test loss: 0.2051, Test accuracy: 79.60%
-------------------------------------------------------------

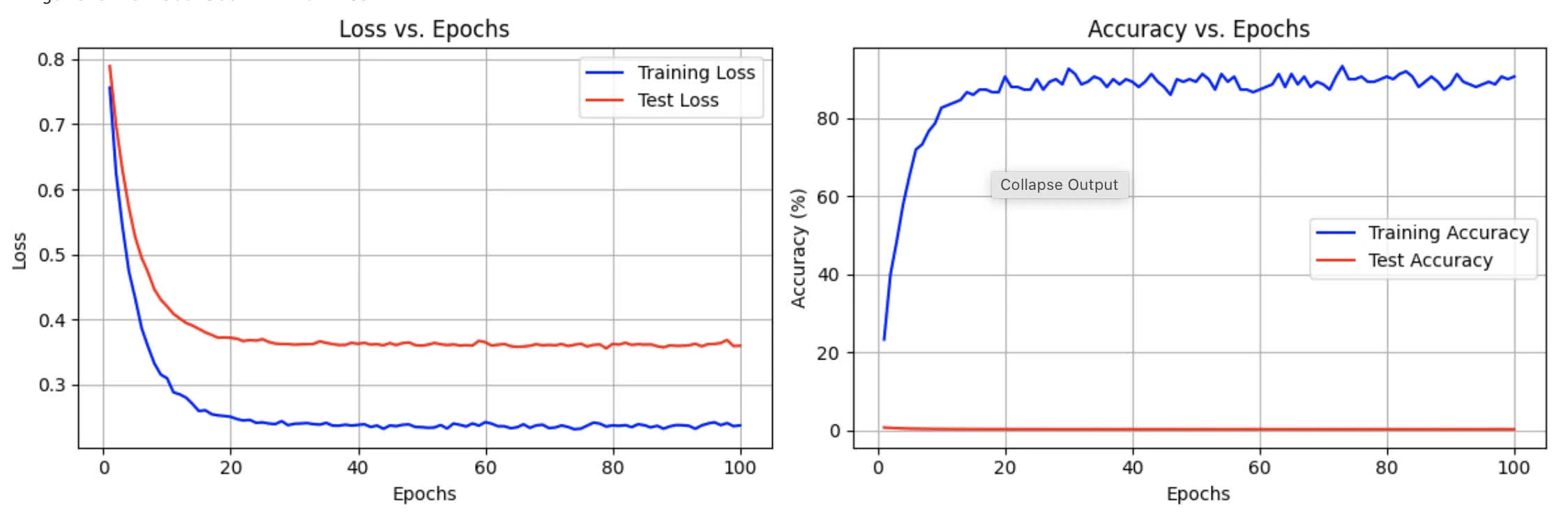
Training with weight decay = 1
=============================================================
Epoch 020 - Train loss: 0.2499, Train accuracy: 90.67%
          - Test loss: 0.3714, Test accuracy: 73.00%
-------------------------------------------------------------
Epoch 040 - Train loss: 0.2374, Train accuracy: 89.33%
          - Test loss: 0.3621, Test accuracy: 73.30%
-------------------------------------------------------------
Epoch 060 - Train loss: 0.2416, Train accuracy: 87.33%
          - Test loss: 0.3646, Test accuracy: 72.80%
-------------------------------------------------------------
Epoch 080 - Train loss: 0.2367, Train accuracy: 90.67%
          - Test loss: 0.3621, Test accuracy: 74.70%
-------------------------------------------------------------
Epoch 100 - Train loss: 0.2366, Train accuracy: 90.67%
          - Test loss: 0.3592, Test accuracy: 74.20%
-------------------------------------------------------------

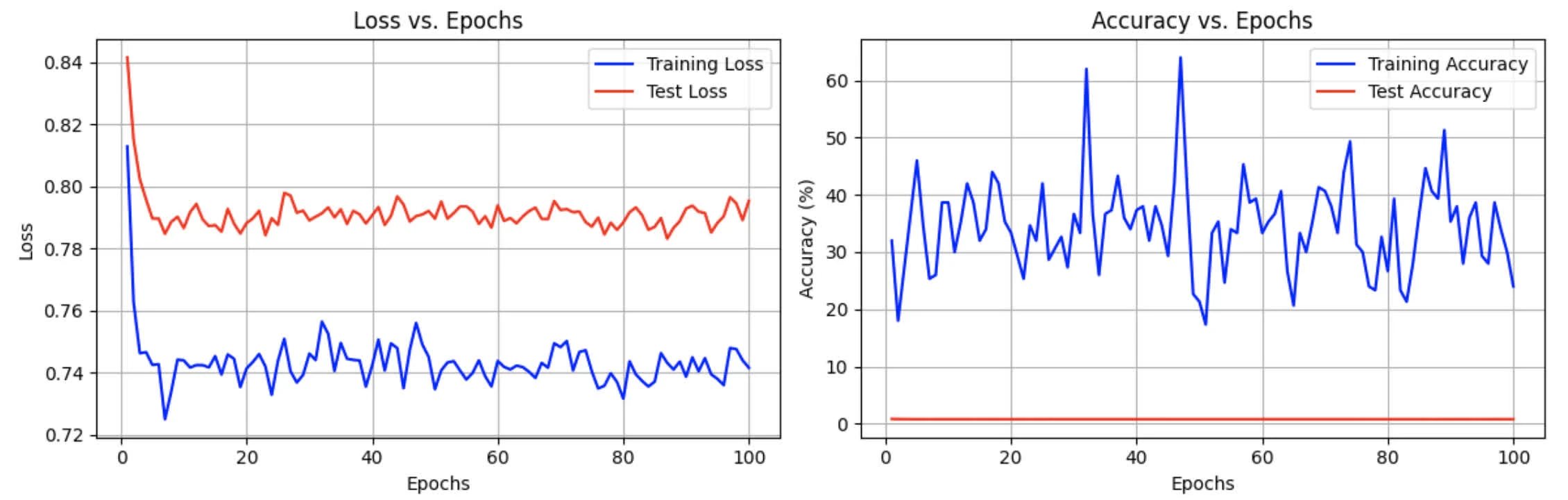
Training with weight decay = 10
=============================================================
Epoch 020 - Train loss: 0.7413, Train accuracy: 33.33%
          - Test loss: 0.7881, Test accuracy: 23.10%
-------------------------------------------------------------
Epoch 040 - Train loss: 0.7422, Train accuracy: 37.33%
          - Test loss: 0.7906, Test accuracy: 22.00%
-------------------------------------------------------------
Epoch 060 - Train loss: 0.7437, Train accuracy: 33.33%
          - Test loss: 0.7938, Test accuracy: 18.50%
-------------------------------------------------------------
Epoch 080 - Train loss: 0.7316, Train accuracy: 26.67%
          - Test loss: 0.7883, Test accuracy: 16.90%
-------------------------------------------------------------
Epoch 100 - Train loss: 0.7415, Train accuracy: 24.00%
          - Test loss: 0.7953, Test accuracy: 13.70%
-------------------------------------------------------------

final results comparison:
======================================================================
weight decay   train loss    test loss    train acc     test acc
----------------------------------------------------------------------
         0.1       0.0422       0.2051       99.33%       79.60%
         1.0       0.2366       0.3592       90.67%       74.20%
        10.0       0.7415       0.7953       24.00%       13.70%

Yes, but the result is highly sensitive based on given weight decay value.

1. with weight_decay = 0.1 we observe the best performance, with training accuracy reaches to 99.33%, smaller gap between train and test loss. Smooth learning curves with stable conversion.
2. with weight_decay = 1 we saw a decrease in training accuracy, larger gap between training and test loss, training become a bit unstable with fluctuation in accuracy, and regularisation is too strong, which affect learning
3. with weight_decay = 10, we saw it severely impairs model performance, given that it is too restrictive. Unstable training, high loss values, regularisation is too aggressive.

Small dataset makes the model more sensitive to regularisation. Linearity makes it lax to require regularisation.

Weight decay does help when properly tuned, and make learning a bit more stable.

task 2: Logistic Regression for MNIST classification

part a

Use Cross Entropy Loss (rather than Hinge loss) to implement logistic regression

context:

• Hinge Loss: it penalized predictions that are not sufficiently confident. Only cares about correct classification with sufficient margin

• cross-entropy:

  For binary loss is defined:

  $$L(y, p(x)) = -(y * \log(p(x)) + (1-y) * \log (1-p(x)))$$

  For multi-class is defined:

  $$L(y, p(x)) = - \sum y_i * \log(p_i(x))$$

part b

1. Compute the accuracy on the train and test set after each epoch in the training. Plot these accuracies as a function of the epoch number.
2. Compute the cross-entropy loss on the train and test set after each epoch in the training. Plot these loss values as a function of the epoch number.
3. Report the last epoch results (including loss values and accuracies) for both train and test sets.
4. Does the model shows significant overfitting? Or do you think there might be other factors that are more significant in the mediocre performance of the model?

The following is the graph entails both accuracy and loss on train/test dataset:

-------------------------------------------------------------
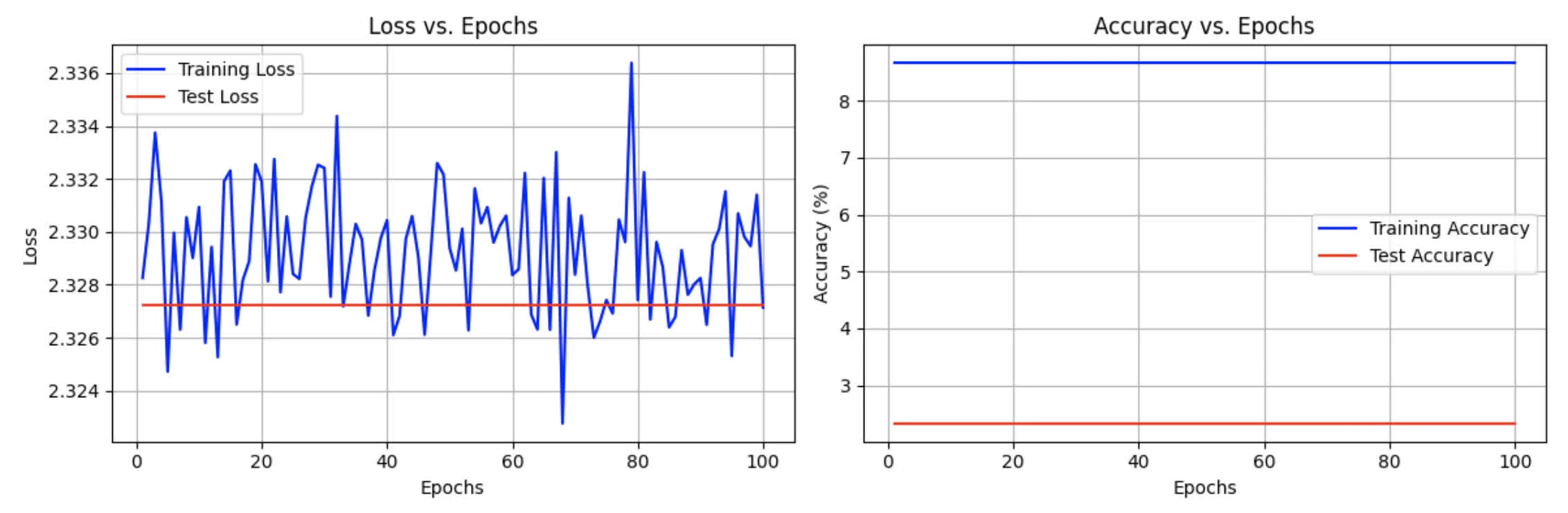
Epoch 100 - Train loss: 2.3271, Train accuracy: 8.67%
          - Test loss: 2.3272, Test accuracy: 8.20%
-------------------------------------------------------------

No sign of overfitting, given training/test accuracy are very close together. Training loss and test loss curves are pretty close

The reason for poor performance are as follow:

• random chance baseline: for 10-class problem, random guessing would give ~10% accuracy, so it perform a bit worse.
• The model doesn’t seem to learn at all. It perform significantly worse than SVM.
• Cross-entropy loss might need additional tuning.
• Non-linearity: Given that MNIST data contains non-linear features, it might be hard for LR to capture all information from training dataset.

part c

Does it work better, worse, or similar?

Significantly worse, due to the difference in loss function.

task 3: non-linearity

part a

Add a hidden layer with 5000 neurons and a RELU layer for both logistic regression and SVM models in Task 1 and Task 2.

1. For both models, plot the train loss and the test loss.
2. For both models, plot the train and test accuracies.
3. For both models, report the loss and accuracy for both train and test sets.

The following is the modified version of LinearSVM with hidden layers:

class ModifiedModel(nn.Module):
  def __init__(self, input_size, hidden_size, num_classes):
    super().__init__()
    self.fc1 = nn.Linear(input_size, hidden_size)
    self.relu = nn.ReLU()
    self.fc2 = nn.Linear(hidden_size, num_classes)
 
  def forward(self, x):
    x = x.view(-1, input_size)
    x = self.fc1(x)
    x = self.relu(x)
    return self.fc2(x)

With training/test accuracy and loss graph:

Final epoch result:

------------------------------------------------------------
Epoch 100:
Train Loss: 0.0033, Train Accuracy: 100.00%
Test Loss: 0.1723, Test Accuracy: 78.10%
------------------------------------------------------------

Modified version of LogisticRegression with hidden layers:

class ModifiedLogisticModel(nn.Module):
  def __init__(self, input_size, hidden_size, num_classes):
    super().__init__()
    self.fc1 = nn.Linear(input_size, hidden_size)
    self.relu = nn.ReLU()
    self.fc2 = nn.Linear(hidden_size, num_classes)
 
  def forward(self, x):
    x = x.view(-1, input_size)
    x = self.fc1(x)
    x = self.relu(x)
    return self.fc2(x)

With training/test accuracy and loss graph:

Final epoch result:

------------------------------------------------------------
Epoch 100:
Train Loss: 0.1133, Train Accuracy: 100.00%
Test Loss: 0.6675, Test Accuracy: 78.70%
------------------------------------------------------------

part b

Compare the results with the linear model (without weight decay, to keep the comparison fair). Which approach works better? Why? Which appproach is more prone to overfitting? Explain your findings and justify it.

Linear model works better in this case, even thought it achieve lower loss, similar test accuracy. The added complexity of the hidden layer and ReLU activation didn’t improve the model’s performance given the dataset size (too small)

The problem set might be linearly separable enough such that the model simply learns to generalise overall behaviour of the whole dataset (also known as grokking ⁴).

Note that overfitting suggests that there weren’t enough data in given training sets, given we observe similar test metrics for both LinearSVM and ModifiedModel (with ReLU and hidden layers)

So it is not necessary “which works better”, rather it should be about limited training data rather than architectural options.

task 4: data augmentation

instruction

In this task, we will explore the concept of data augmentation, which is a powerful technique used to enhance the diversity of our training dataset without collecting new data. By applying various transformations to the original training images, we can create modified versions of these images. We can then use these modified images to train our model with a “richer” set of examples. The use of data augmentation helps to improve the robustness and generalization of our models. Data augmentation is particularly beneficial in tasks like image classification, where we expect the model to be invariant to slight variations of images (e.g., rotation, cropping, blurring, etc.)

For this task, you are given a code that uses Gaussian Blur augmentation, which applies a Gaussian filter to slightly blur the images. If you run the code, you will see that this type of augmentation actually makes the model less accurate (compared with Task 3, SVM test accuracy)

For this task, you must explore other types of data augmentation and find one that improves the test accuracy by at least 1 percent compared with not using any augmentation (i.e., compared with Task 3, SVM test accuracy). Only change the augmentation approach, and keep the other parts of the code unchanged. Read the PyTorch documentation on different augmentation techniques here, and then try to identify a good augmentation method from them.

Report the augmentation approach that you used, and explain why you think it helps. Also include train/test accuracy plots per epoch, and the train/test accuracy at the final epoch.

The following augmentation achieves higher test accuracy comparing to ModifiedModel without any transformation

augmentation = transforms.Compose([
  # Small random rotation with higher probability of small angles
  transforms.RandomRotation(degrees=3, fill=0),  # Even more conservative rotation
  # Very subtle random perspective
  transforms.RandomPerspective(distortion_scale=0.15, p=0.3, fill=0),
  # Convert to tensor
  transforms.ToTensor(),
  # Normalize to improve training stability
  transforms.Normalize((0.1307,), (0.3081,)),  # MNIST mean and std
  # Extremely subtle random noise
  transforms.RandomAdjustSharpness(sharpness_factor=1.2, p=0.3)
])

Explanation

ToTensor is self-explanatory. Additional augmentation playground can also be found in the jupyter notebook

RandomRotation

• we use $+-3$ degrees given that digits can appear at slightly different angles in said dataset
• small rotation preserves readability, while increase variety
• fill set to 0 to preserve black background

RandomPerspective

• add a small distortion scale to simulate viewing angle variations.
• help with robustness to viewpoint change

Normalise

• Add MNIST mean and std to normalise training
• make it more stable

RandomAdjustSharpness

• Simulate some random noise
• One can also use RandomErasing, but the essentially work the same

results

The following is the final epoch result:

-------------------------------------------------------------
Epoch 100 - Train loss: 0.015159, Train accuracy: 99.33%
         - Test loss: 0.183071, Test accuracy: 81.10%
-------------------------------------------------------------

With graphs:

Footnotes

1. Loss is defined as: $\text{loss}(x,y) = \frac{\sum_{i} \max{0, \text{margin} - x[y] + x[i]}^p}{x.\text{size}(0)}$ ↩

2. Given input $(x_1, y_1), \ldots, (x_m, y_m)$

   parameters:

   • regularization parameter $\lambda > 0$
   • loss function $\delta: \mathcal{Y} \times \mathcal{Y} \rightarrow \mathbb{R}_{+}$
   • class sensitive feature mapping $\Psi: \mathcal{X} \times \mathcal{Y} \rightarrow \mathbb{R}^d$

   In this case, we solve for

   $$\min_{w \in \mathbb{R}^d} (\lambda \|w\|^2 + \frac{1}{m} \sum_{i=1}^{m} \max_{y^{'} \in \mathcal{Y}}(\delta (y^{'}, y_i) + \langle w, \Psi (x_i, y^{'}) - \Psi (x_i, y_i) \rangle))$$ ↩

3. MNIST datasets are 60000 28x28 grayscale images, therefore $0.25/100 * 60000 = 150$ samples being used ↩

4. grokking is a process where neural network learns a pattern in the data, and it “memorize” this pattern to generalize to all unseen dataset, in which improve generalisation performance from random chance to perfect generalisation! Though, this phenomena is often observed in larger networks beyond overfitting. ↩