---
date: '2024-10-31'
description: A list of optimization functions that can be used in ML training to reduce loss, and more.
id: optimization
modified: 2026-06-05 15:08:07 GMT-04:00
tags:
  - ml
title: ml optimization
created: '2024-10-31'
published: '2024-10-31'
pageLayout: default
slug: thoughts/optimization
permalink: https://aarnphm.xyz/thoughts/optimization.md
generator:
  quartz: v4.6.0
  hostedProvider: Cloudflare
  baseUrl: aarnphm.xyz
full: https://aarnphm.xyz/llms-full.txt
---
## softmax

$$
\text{softmax(y)}_i = \frac{e^{y_i}}{\sum_{i} e^{y_i}}
$$

where $y \in \mathbb{R}^k$

> \[!tip\] numerical stability (log‑sum‑exp)
>
> Always subtract the max logit: with $m = \max_j y_j$,
>
> $$
> p_i = \frac{e^{y_i - m}}{\sum_j e^{y_j - m}}, \qquad
> \log p_i = y_i - \operatorname{LSE}(y),\quad \operatorname{LSE}(y)=\log\sum_j e^{y_j}.
> $$

see also: <https://leimao.github.io/blog/Online-Safe-Softmax/> \[@milakov2018onlinenormalizercalculationsoftmax\], used with [[thoughts/Attention|Flash Attention]]

### Jacobian and gradients

Jacobian of softmax $p=\text{softmax}(y)$:

$$
\frac{\partial p_i}{\partial y_j} = p_i(\delta_{ij} - p_j) \;\equiv\; \operatorname{diag}(p) - pp^\top.
$$

Cross‑entropy with hard label $y^*$: $L=-\log p_{y^*}$. Gradient w\.r.t. logits:

$$
\frac{\partial L}{\partial y} = p - \operatorname{one\_hot}(y^*).
$$

For soft targets $t \in \Delta^k$, $L=-\sum_i t_i \log p_i$ gives $\partial L/\partial y = p - t$.

> \[!see-also\] links
>
> - Binary special case: [[thoughts/Logistic regression#MLE derivation and gradients]].
> - Training view: [[thoughts/Maximum likelihood estimation#training statistical models (derivation sketch)]].

## `exp()`

@abdelkhalik2022demystifyingnvidiaamperearchitecture, [RDNA3 instruction sets of V\_LDEXP\_F32](https://www.amd.com/content/dam/amd/en/documents/radeon-tech-docs/instruction-set-architectures/rdna3-shader-instruction-set-architecture-feb-2023_0.pdf)

Usually a lot better comparing to `2**t` simply for [[thoughts/university/twenty-three-twenty-four/compsci-4x03/Equations|numerical stability]] reasons

For ARM the design specially [instructions](https://developer.arm.com/documentation/ddi0602/2024-09/SVE-Instructions/FEXPA--Floating-point-exponential-accelerator-) set for it!

```cpp title="pseudocode-exp-fexpa.cpp"
// Pseudocode representing the computation flow:
float32x4_t exp_sve2(float32x4_t x) {
    // Step 1: Range reduction
    // N = round(x * log2(e))
    // r = x - N * ln(2)    [reduced argument]

    // Step 2: FEXPA instruction provides 2^N approximation
    // In hardware: FEXPA Z0.S, Z1.S
    float32x4_t exp_approx; // Result of FEXPA

    // Step 3: Polynomial evaluation for exp(r)
    // Typically uses Horner's method with reduced precision
    // coefficients since we're starting with a good approximation
    float32x4_t exp_r = evaluate_polynomial(r);

    // Step 4: Combine results
    return exp_approx * exp_r;
}
```

Advantages of FEXPA:

- single instruction latency for initial approximation
- vectorized ops for batch processing

On GPU we can utilise bit-shift `1<<x` or CUDA’s exp2

Optimization in `llama.cpp`: [ggerganov/llama.cpp#7154](https://github.com/ggerganov/llama.cpp/pull/7154)

## RoPE

\[@su2023roformerenhancedtransformerrotary\{pg.V\}\]

## sigmoid

$$
\text{sigmoid}(x) = \frac{1}{1+e^{-x}}
$$

## ReLU

$$
\text{FFN}(x, W_{1}, W_{2}, b_{1}, b_{2}) = max(0, xW_{1}+b_{1})W_{2} + b_{2}
$$

A version in T5 without bias:

$$
\text{FFN}_\text{ReLU}(x,W_{1},W_{2}) = max(xW_{1},0)W_{2}
$$

## Swish

@ramachandran2017searchingactivationfunctions introduces an alternative to ReLU that works better on deeper models across different tasks.

$$
f(x) = x \cdotp \text{sigmoid}(\beta x)
\\
\because \beta : \text{ constant parameter}
$$

## Gated Linear Units and Variants

> component-wise product of two linear transformations of the inputs, one of which is sigmoid-activated.

@shazeer2020gluvariantsimprovetransformer introduces a few GELU activations to yield improvements in [[thoughts/Transformers]] architecture.

$$
\begin{aligned}
\text{GLU}(x,W,V,b,c) &= \sigma(xW+b) \otimes (xV+c) \\
\text{Bilinear}(x,W,V,b,c) &= (xW+b) \otimes (xV+c)
\end{aligned}
$$

GLU in other variants:

$$
\begin{aligned}
\text{ReGLU}(x,W,V,b,c) &= \max(0, xW+b) \otimes (xV+c) \\
\text{GEGLU}(x,W,V,b,c) &= \text{GELU}(xW+b) \otimes (xV+c) \\
\text{SwiGLU}(x,W,V,b,c) &= \text{Swish}_\beta(xW+b) \otimes (xV+c)
\end{aligned}
$$

FFN for transformers layers would become:

$$
\begin{aligned}
\text{FFN}_\text{GLU}(x,W,V,W_{2}) &= (\sigma (xW) \otimes xV)W_{2} \\
\text{FFN}_\text{Bilinear}(x,W,V,W_{2}) &= (xW \otimes xV)W_{2} \\
\text{FFN}_\text{ReGLU}(x,W,V,W_{2}) &= (\max(0, xW) \otimes xV)W_{2} \\
\text{FFN}_\text{GEGLU}(x,W,V,W_{2}) &= (\text{GELU}(xW) \otimes xV)W_{2} \\
\text{FFN}_\text{SwiGLU}(x,W,V,W_{2}) &= (\text{Swish}_\beta(xW) \otimes xV)W_{2}
\end{aligned}
$$

_note_: reduce number of hidden units $d_\text{ff}$ (second dimension of $W$ and $V$ and the first dimension of $W_{2}$) by a factor of $\frac{2}{3}$ when comparing these layers

## JumpReLU

@erichson2019jumpreluretrofitdefensestrategy proposes JumpRELU to address robustness through adversarial examples.

@rajamanoharan2024jumpingaheadimprovingreconstruction then apply this to improves construction fielity as [[thoughts/sparse autoencoder#Gated SAE]]

$$
J(z) \coloneqq z H(z - \kappa) = \begin{cases} 0 & \text{if } z \leq \kappa \\ z & \text{if } z > \kappa \end{cases}
$$

![[thoughts/images/JumpReLU.mp4]]

## Newton methods

Second‑order step with gradient $g=\nabla f(\theta)$ and Hessian $H=\nabla^2 f(\theta)$:

$$
\theta_{t+1} = \theta_t - H(\theta_t)^{-1} g(\theta_t).
$$

- For convex $f$, converges quadratically near optimum.
- In practice use approximations: L‑BFGS, conjugate gradients, or Fisher‐scoring/natural‑gradient with Fisher $F \approx H$.

## momentum

See also [[thoughts/university/twenty-four-twenty-five/sfwr-4ml3/Stochastic gradient descent|SGD]], [Cornell’s CS6787](https://www.cs.cornell.edu/courses/cs6787/2017fa/Lecture3.pdf), [[thoughts/gradient descent]]

In the case of quadratic function: $f(x) = \frac{1}{2} x^2$, then $x_{t+1} = x_t - \alpha x_t = (1-\alpha)x_t$

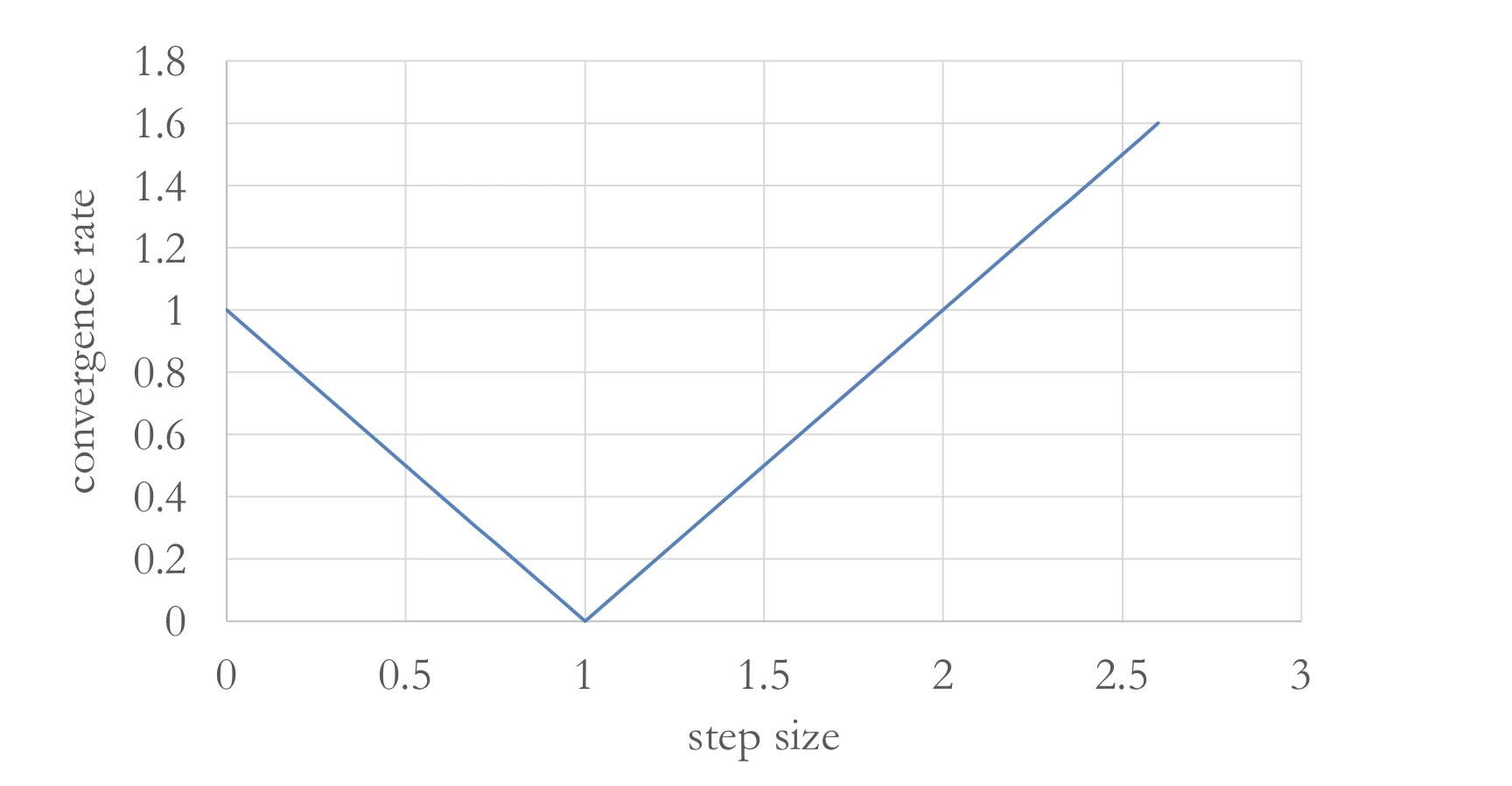
Think of convergence rate

$$
\mid x_{t+1} - 0 \mid = \mid  1 - \alpha \mid \mid  x_t - 0 \mid
$$

![[thoughts/images/convergence-vs-step-side-momentum.webp]]

If we set different curvature ($f(x) = 2x^2$) thus $x_{t+1} = x_t - 4 \alpha x_t = (1-4 \alpha)x_t$

> \[!tip\] step size
>
> step size depends on curvature for one-dimensional quadratics
>
> more curvature means smaller ideal step size

_how would this play for general quadratics?_

for PSD symmetric $A$

$$
f(x) = \frac{1}{2} x^T Ax
$$

with gradient descent has update step

$$
x_{t+1} = x_t - \alpha  A x_t = (I - \alpha A)x_t
$$

convergence rate would be

$$
\begin{aligned}
\max_{x} \frac{\|(I - \alpha A)x\|}{\|x\|} &= \max_{x} \frac{1}{\|x\|} \left\| \left( I - \alpha \sum_{i=1}^{n} \lambda_i u_i u_i^T \right) x \right\| \\[8pt]
&= \max_{x} \frac{\|\sum_{i=1}^{n} (1- \alpha \lambda_i) u_i u_i^T x\|}{\|\sum_{i=1}^{n} u_i u_i^T x\|} \\
&= max_i \mid 1- \alpha \lambda_i \mid  \\
&=max(1-\alpha \lambda_{\text{min}}, \alpha \lambda_{\text{max}} - 1)
\end{aligned}
$$

> \[!math\] 1. optimal convergence rate
>
> optimal value occurs when
>
> $$
> 1 - \alpha \lambda_{\text{min}} = \alpha \lambda_{\text{max}} - 1 \Rightarrow \alpha = \frac{2}{\lambda_{\text{max}} + \lambda_{\text{min}}}
> $$
>
> with rate
>
> $$
> \frac{\lambda_{\text{max}} - \lambda_{\text{min}}}{\lambda_{\text{max}} + \lambda_{\text{min}}}
> $$

We denote $\kappa = \frac{\lambda_{\text{max}}}{\lambda_{\text{min}}}$ as **condition number** of matrix A

> \[!abstract\] poorly conditioned
>
> Problems with larger condition numbers converge slower.
>
> Intuitively these are problems that are <mark>highly curved in some directions, but flat others</mark>

### Polyak

abbreviation: “heavy ball method”

idea: add an extra momentum term to gradient descent

$$
x_{t+1} = x_t - \alpha \nabla f(x_t) + \beta (x_t - x_{t-1})
$$

tl/dr: if current gradient step is in same direction as previous step, then move a little further in the same direction

> \[!math\]- 2. momentum for 1D quadratics
>
> $$
> f(x) = \frac{\lambda}{2} x^{2}
> $$
>
> momentum GD gives
>
> $$
> \begin{aligned}
> x_{t+1} &= x_t - \alpha \lambda x_t + \beta (x_t - x_{t-1}) \\
> &= (1+\beta - \alpha \lambda) x_t - \beta x_{t-1}
> \end{aligned}
> $$
>
> characterizing momentum:
>
> - start with $x_{t+1} = (1+\beta -\alpha \lambda) x_t - \beta x_{t-1}$
> - trick: let $x_t = \beta^{t/2}z_t$
>
> $$
> z_{t+1} = \frac{1 + \beta - \alpha \lambda}{\sqrt{\beta}} z_t - z_{t-1}
> $$
>
> let $u = \frac{1+\beta -\alpha \lambda}{2 \sqrt{\beta}}$, then
>
> $$
> z_{t+1} = 2 u z_t - z_{t-1}
> $$
>
> _degree-$\textbf{t}$ polynomial in $\textbf{u}$_

### nesterov

![[thoughts/Nesterov momentum]]

### RMSNorm

see also \[@zhang2019rootmeansquarelayer\]

motivation: LayerNorm helps stabilize training

implementations in PyTorch:

$$
y_{i} = \frac{x_{i}}{\text{RMS}(x)} \times \gamma_{i} \text{ where } \text{RMS}(x) = \sqrt{\epsilon + \frac{1}{n} \sum_{i=1}^{n} x_i^2}
$$

### modular duality

@bernstein2024modulardualitydeeplearning

<https://docs.modula.systems/algorithms/newton-schulz/>

### muon

![[thoughts/muon]]