--- date: '2024-02-26' description: graph theory covering directed and undirected graphs, adjacency lists, dfs and bfs traversal, connected components, bipartite graphs, shortest paths. id: Graphs modified: 2026-06-05 15:08:41 GMT-04:00 tags: - sfwr2c03 title: Graphs created: '2024-02-26' published: '2024-02-26' pageLayout: default slug: thoughts/university/twenty-three-twenty-four/sfwr-2c03/Graphs permalink: https://aarnphm.xyz/thoughts/university/twenty-three-twenty-four/sfwr-2c03/Graphs.md generator: quartz: v4.6.0 hostedProvider: Cloudflare baseUrl: aarnphm.xyz full: https://aarnphm.xyz/llms-full.txt --- See also [[thoughts/university/sfwr-2c03/graph-algo.pdf|slides]] _Node_ as [[thoughts/Information Theory|information]] and _edges_ as relationship between [[thoughts/data|data]] ## Directed acyclic graph (DAG) Application: [[thoughts/Merkle DAG|Merkle DAG]] ## undirected. > \[!note\] `(\mathcal{N}, \mathcal{E})` > > - $\mathcal{N}$: set of vertices > - $\mathcal{E}$: set of _undirected_ edges: $\mathcal{E} \subseteq \mathcal{N} \times \mathcal{N}$ _path_ is a sequence of nodes and edges connect two nodes. > A graph is **connected** if there is a path between every pair of vertices. In a weight undirected graph each edge has a weight: $w: \mathcal{E} \to \mathbb{R}$ See also [[thoughts/Group theory#Graph isomorphism|Graph isomorphism]] ## directed. > \[!note\] `(\mathcal{N}, \mathcal{E})` > > - $\mathcal{N}$: set of vertices > - $\mathcal{E}$: set of edges containing node pairs: $\mathcal{E} \subseteq \mathcal{N} \times \mathcal{N}$ > \[!tip\] _path_ difference > > sequence of nodes and edges are directional, edges are ordered pairs. > \[!note\] _cycle_ > > path with at-least one edge from a node > **Strongly component**: maximal sub-graph in which all node pairs are strongly connected. ## matrix [[thoughts/representations|representation]] Let $\mathcal{G} = (\mathcal{N}, \mathcal{E})$ be a directed graph with $n \in \mathcal{N} \land id(n) \text{ with } 0 \leq id(n) \leq |\mathcal{N}|$ Let $M = | \mathcal{N} | \times | \mathcal{N} |$ matrix > For every pairs of nodes $(m, n)$ set $M[id(m), id(n)] \coloneqq (m, n) \in \mathcal{E}$ ## The adjacency list representation > \[!tip\] Important > > Let $A \lbrack 0 \dots |\mathcal{N}|$ be an array of _bags_ > For every edge $(m, n \in \mathcal{E})$ add $n$ to $(m,n)$ to bag $A \lbrack id(m) \rbrack$ | ops | complexity | | ---------------------------------------- | ----------------------------------------- | | add/remove nodes | $\Theta(\|\mathcal{N}\|)$ (copy array) | | add/remove edges $(n, m)$ | $\Theta(\|out(n)\|)$ (adding to bag) | | check an edge $(n, m)$ exists | $\Theta(\|out(n)\|)$ (searching bags) | | iterate over all _incoming_ edges of $n$ | $\Theta(\|\mathcal{E}\|)$ (scan all bags) | | iterate over all _outgoing_ edges of $n$ | $\Theta(\|out(n)\|)$ (scan a bag) | | Check or change the weight of $(n, m)$ | $\Theta(1)$ | ## comparison. > **Dense** graph: $|\mathcal{E}| \approx \Theta(|\mathcal{N}|^2)$ > **Sparse** graph: $|\mathcal{E}| \approx \Theta(|\mathcal{N}|)$ ## Traversing undirected graph. ### Depth-first search (DFS) ![[thoughts/university/twenty-three-twenty-four/sfwr-2c03/images/example-graph-dfs.webp]]
"\\begin{algorithm}\n\\caption{DFS-R(G, marked, n)}\n\\begin{algorithmic}\n\\REQUIRE $G = (\\mathcal{N}, \\mathcal{E}), \\text{marked}, n \\in \\mathcal{N}$\n\\FORALL{$ (n, m) \\in \\mathcal{E} $}\n \\IF{$\\neq \\text{marked}[m]$}\n \\STATE $\\text{marked}[m] \\coloneqq \\text{true}$\n \\STATE $\\text{DFS-R}{(G, \\text{marked}, m)}$\n \\ENDIF\n\\ENDFOR\n\\end{algorithmic}\n\\end{algorithm}"

Algorithm 1 DFS-R(G, marked, n)

Require: G=(N,E),marked,n∈NG = (\mathcal{N}, \mathcal{E}), \text{marked}, n \in \mathcal{N}

1:for all (n,m)∈E (n, m) \in \mathcal{E} do

2:if ≠marked[m]\neq \text{marked}[m] then

3:marked[m]≔true\text{marked}[m] \coloneqq \text{true}

4:DFS-R(G,marked,m)\text{DFS-R}{(G, \text{marked}, m)}

5:end if

6:end for

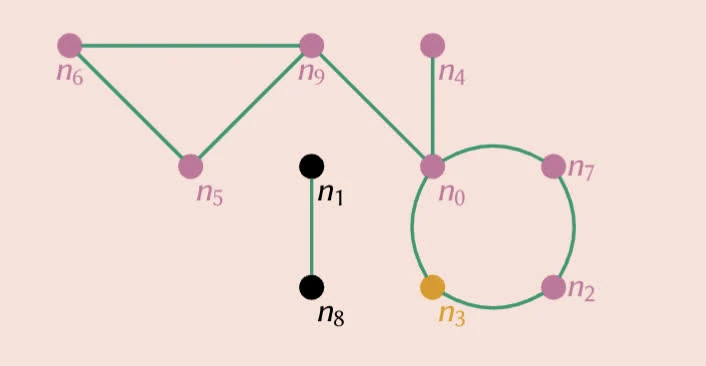
$\text{marked} \coloneqq \lbrace n \longmapsto (n \neq s) \mid n \in \mathcal{N} \rbrace$ > \[!tip\] Conclusion > > - all nodes to which $n_3$ is connected > - $\mathcal{G}$ is **not** a connected graph > - The order of recursive call determines all $n_3$ is connected to. #### Complexity - $|\mathcal{N}|$ memory for _marked_ and at-most $|\mathcal{N}|$ recursive calls - inspect each node at-most once and traverse each edge once: $\Theta(|\mathcal{N}| + |\mathcal{E}|)$ #### Connected-components
"\\begin{algorithm}\n\\caption{DFS-CC-R(G, cc, n)}\n\\begin{algorithmic}\n\\REQUIRE $G = (\\mathcal{N}, \\mathcal{E}), cc, n \\in \\mathcal{N}$\n\\FORALL{$(n, m) \\in \\mathcal{E}$}\n \\IF{$cc[m] = \\text{unmarked}$}\n \\STATE $cc[m] \\coloneqq cc[n]$\n \\STATE $\\text{DFS-CC-R}(G, cc, m)$\n \\ENDIF\n\\ENDFOR\n\\end{algorithmic}\n\\end{algorithm}"

Algorithm 2 DFS-CC-R(G, cc, n)

Require: G=(N,E),cc,n∈NG = (\mathcal{N}, \mathcal{E}), cc, n \in \mathcal{N}

1:for all (n,m)∈E(n, m) \in \mathcal{E} do

2:if cc[m]=unmarkedcc[m] = \text{unmarked} then

3:cc[m]≔cc[n]cc[m] \coloneqq cc[n]

4:DFS-CC-R(G,cc,m)\text{DFS-CC-R}(G, cc, m)

5:end if

6:end for

"\\begin{algorithm}\n\\caption{COMPONENTS(G, s)}\n\\begin{algorithmic}\n\\REQUIRE $G = (\\mathcal{N}, \\mathcal{E}), s \\in \\mathcal{N}$\n\\STATE $cc \\coloneqq \\{ n \\mapsto \\text{unmarked} \\}$\n\\FORALL{$n \\in \\mathcal{N}$}\n \\IF{$cc[n] = \\text{unmarked}$}\n \\STATE $cc[n] \\coloneqq n$\n \\STATE $\\text{DFS-CC-R}(G, cc, n)$\n \\ENDIF\n\\ENDFOR\n\\end{algorithmic}\n\\end{algorithm}"

Algorithm 3 COMPONENTS(G, s)

Require: G=(N,E),s∈NG = (\mathcal{N}, \mathcal{E}), s \in \mathcal{N}

1:cc≔{n↦unmarked}cc \coloneqq \{ n \mapsto \text{unmarked} \}

2:for all n∈Nn \in \mathcal{N} do

3:if cc[n]=unmarkedcc[n] = \text{unmarked} then

4:cc[n]≔ncc[n] \coloneqq n

5:DFS-CC-R(G,cc,n)\text{DFS-CC-R}(G, cc, n)

6:end if

7:end for

#### Two-colourability > \[!tip\] Bipartite graph > > A graph is _bipartite_ if we can partition the nodes in two sets such that no two nodes in the same set share an edge.
"\\begin{algorithm}\n\\caption{DFS-TC-R(G, colors, n)}\n\\begin{algorithmic}\n\\REQUIRE $G = (\\mathcal{N}, \\mathcal{E}), \\text{colors}, n \\in \\mathcal{N}$\n\\FORALL{$(n, m) \\in \\mathcal{E}$}\n \\IF{$\\text{colors}[m] = 0$}\n \\STATE $\\text{colors}[m] \\coloneqq -\\text{colors}[n]$\n \\STATE $\\text{DFS-TC-R}(G, \\text{colors}, m)$\n \\ELSIF{$\\text{colors}[m] = \\text{colors}[n]$}\n \\STATE \\textbf{print} \"This graph is not bipartite.\"\n \\ENDIF\n\\ENDFOR\n\\end{algorithmic}\n\\end{algorithm}"

Algorithm 4 DFS-TC-R(G, colors, n)

Require: G=(N,E),colors,n∈NG = (\mathcal{N}, \mathcal{E}), \text{colors}, n \in \mathcal{N}

1:for all (n,m)∈E(n, m) \in \mathcal{E} do

2:if colors[m]=0\text{colors}[m] = 0 then

3:colors[m]≔−colors[n]\text{colors}[m] \coloneqq -\text{colors}[n]

4:DFS-TC-R(G,colors,m)\text{DFS-TC-R}(G, \text{colors}, m)

5:else if colors[m]=colors[n]\text{colors}[m] = \text{colors}[n] then

6:print "This graph is not bipartite."

7:end if

8:end for

"\\begin{algorithm}\n\\caption{TwoColors(G)}\n\\begin{algorithmic}\n\\REQUIRE $G = (\\mathcal{N}, \\mathcal{E})$\n\\STATE $\\text{colors} \\coloneqq \\{ n \\mapsto 0 \\mid n \\in \\mathcal{N} \\}$\n\\FORALL{$n \\in \\mathcal{N}$}\n \\IF{$\\text{colors}[n] = 0$}\n \\STATE $\\text{colors}[n] \\coloneqq 1$\n \\STATE $\\text{DFS-TC-R}(G, \\text{colors}, n)$\n \\ENDIF\n\\ENDFOR\n\\end{algorithmic}\n\\end{algorithm}"

Algorithm 5 TwoColors(G)

Require: G=(N,E)G = (\mathcal{N}, \mathcal{E})

1:colors≔{n↦0∣n∈N}\text{colors} \coloneqq \{ n \mapsto 0 \mid n \in \mathcal{N} \}

2:for all n∈Nn \in \mathcal{N} do

3:if colors[n]=0\text{colors}[n] = 0 then

4:colors[n]≔1\text{colors}[n] \coloneqq 1

5:DFS-TC-R(G,colors,n)\text{DFS-TC-R}(G, \text{colors}, n)

6:end if

7:end for

### Breadth-first search (BFS)
"\\begin{algorithm}\n\\caption{BFS(G, s)}\n\\begin{algorithmic}\n\\REQUIRE $G = (\\mathcal{N}, \\mathcal{E}), s \\in \\mathcal{N}$\n\\STATE $\\text{marked} \\coloneqq \\{ n \\mapsto (n \\neq s) \\mid n \\in \\mathcal{N} \\}$\n\\STATE $Q \\coloneqq \\text{a queue holding only } s$\n\\WHILE{$\\neg\\text{Empty}(Q)$}\n \\STATE $n \\coloneqq \\text{Dequeue}(Q)$\n \\FORALL{$(n, m) \\in \\mathcal{E}$}\n \\IF{$\\neg\\text{marked}[m]$}\n \\STATE $\\text{marked}[m] \\coloneqq \\text{true}$\n \\STATE $\\text{Enqueue}(Q, m)$\n \\ENDIF\n \\ENDFOR\n\\ENDWHILE\n\\end{algorithmic}\n\\end{algorithm}"

Algorithm 6 BFS(G, s)

Require: G=(N,E),s∈NG = (\mathcal{N}, \mathcal{E}), s \in \mathcal{N}

1:marked≔{n↦(n≠s)∣n∈N}\text{marked} \coloneqq \{ n \mapsto (n \neq s) \mid n \in \mathcal{N} \}

2:Q≔a queue holding only sQ \coloneqq \text{a queue holding only } s

3:while ¬Empty(Q)\neg\text{Empty}(Q) do

4:n≔Dequeue(Q)n \coloneqq \text{Dequeue}(Q)

5:for all (n,m)∈E(n, m) \in \mathcal{E} do

6:if ¬marked[m]\neg\text{marked}[m] then

7:marked[m]≔true\text{marked}[m] \coloneqq \text{true}

8:Enqueue(Q,m)\text{Enqueue}(Q, m)

9:end if

10:end for

11:end while

#### Single-source shortest path > Given an undirected graph _without weight_ and node $s \in \mathcal{N}$, find a shortest path from node $s$ to all nodes $s$ can reach.
"\\begin{algorithm}\n\\caption{BFS-SSSP(G, s)}\n\\begin{algorithmic}\n\\REQUIRE $G = (\\mathcal{N}, \\mathcal{E}), s \\in \\mathcal{N}$\n\\STATE $\\text{distance} \\coloneqq \\{ n \\mapsto \\infty \\mid n \\in \\mathcal{N} \\}$\n\\STATE $\\text{distance}[s] \\coloneqq 0$\n\\STATE $Q \\coloneqq \\text{a queue holding only } s$\n\\WHILE{$\\neg\\text{Empty}(Q)$}\n \\STATE $n \\coloneqq \\text{Dequeue}(Q)$\n \\FORALL{$(n, m) \\in \\mathcal{E}$}\n \\IF{$\\text{distance}[m] = \\infty$}\n \\STATE $\\text{distance}[m] \\coloneqq \\text{distance}[n] + 1$\n \\STATE $\\text{Enqueue}(Q, m)$\n \\ENDIF\n \\ENDFOR\n\\ENDWHILE\n\\end{algorithmic}\n\\end{algorithm}"

Algorithm 7 BFS-SSSP(G, s)

Require: G=(N,E),s∈NG = (\mathcal{N}, \mathcal{E}), s \in \mathcal{N}

1:distance≔{n↦∞∣n∈N}\text{distance} \coloneqq \{ n \mapsto \infty \mid n \in \mathcal{N} \}

2:distance[s]≔0\text{distance}[s] \coloneqq 0

3:Q≔a queue holding only sQ \coloneqq \text{a queue holding only } s

4:while ¬Empty(Q)\neg\text{Empty}(Q) do

5:n≔Dequeue(Q)n \coloneqq \text{Dequeue}(Q)

6:for all (n,m)∈E(n, m) \in \mathcal{E} do

7:if distance[m]=∞\text{distance}[m] = \infty then

8:distance[m]≔distance[n]+1\text{distance}[m] \coloneqq \text{distance}[n] + 1

9:Enqueue(Q,m)\text{Enqueue}(Q, m)

10:end if

11:end for

12:end while