---
date: '2024-12-13'
description: and some more annotations
id: Relational Algebra
modified: 2026-06-05 15:08:42 GMT-04:00
tags:
  - sfwr3db3
title: Relational Algebra
created: '2024-12-13'
published: '2024-12-13'
pageLayout: default
slug: thoughts/university/twenty-four-twenty-five/sfwr-3db3/Relational-Algebra
permalink: https://aarnphm.xyz/thoughts/university/twenty-four-twenty-five/sfwr-3db3/Relational-Algebra.md
generator:
  quartz: v4.6.0
  hostedProvider: Cloudflare
  baseUrl: aarnphm.xyz
full: https://aarnphm.xyz/llms-full.txt
---
| Operator    | Operation              | Example                         |
| ----------- | ---------------------- | ------------------------------- |
| $\sigma_C$  | Selection              | $\sigma_{A=10}(R)$              |
| $\pi_L$     | Projection             | $\pi_{A,B}(R)$                  |
| $\times$    | Cross-Product          | $R_1 \times R_2$                |
| $\bowtie$   | Natural Join           | $R_1 \bowtie R_2$               |
| $\bowtie_C$ | Theta Join             | $R_1 \bowtie_{R_1.A=R_2.A} R_2$ |
| $\rho_R$    | Rename                 | $\rho_S(R)$                     |
| $\delta$    | Eliminate Duplicates   | $\delta(R)$                     |
| $\tau$      | Sort Tuples            | $\tau(R)$                       |
| $\gamma_L$  | Grouping & Aggregation | $\gamma_{A,AVG(B)}(R)$          |

## selection

idea: picking certain row

$$
R_{1} \coloneqq \sigma_C(R_{2})
$$

$C$ is the condition refers to attribute in $R_{2}$

def: $R_{1}$ is all those tuples of $R_{2}$ that satisfies C

## projection

idea: picking certain column

$$
R_{1} \coloneqq  \pi_L(R_{2})
$$

$L$ is the list of attributes from $R_{2}$

$$
\begin{aligned}
R &=
\begin{bmatrix}
A & B \\
1 & 2 \\
3 & 4
\end{bmatrix} \\[8pt]

\pi_{A+B \rightarrow C, A \rightarrow A_1, A \rightarrow A_2}(R) &=
\begin{bmatrix}
C & A_1 & A_2 \\
3 & 1 & 1 \\
7 & 3 & 3
\end{bmatrix}
\end{aligned}
$$

## products

$$
R_{3} \coloneqq  R_{1} \times R_{2}
$$

![[thoughts/university/twenty-four-twenty-five/sfwr-3db3/products-relalg.webp]]

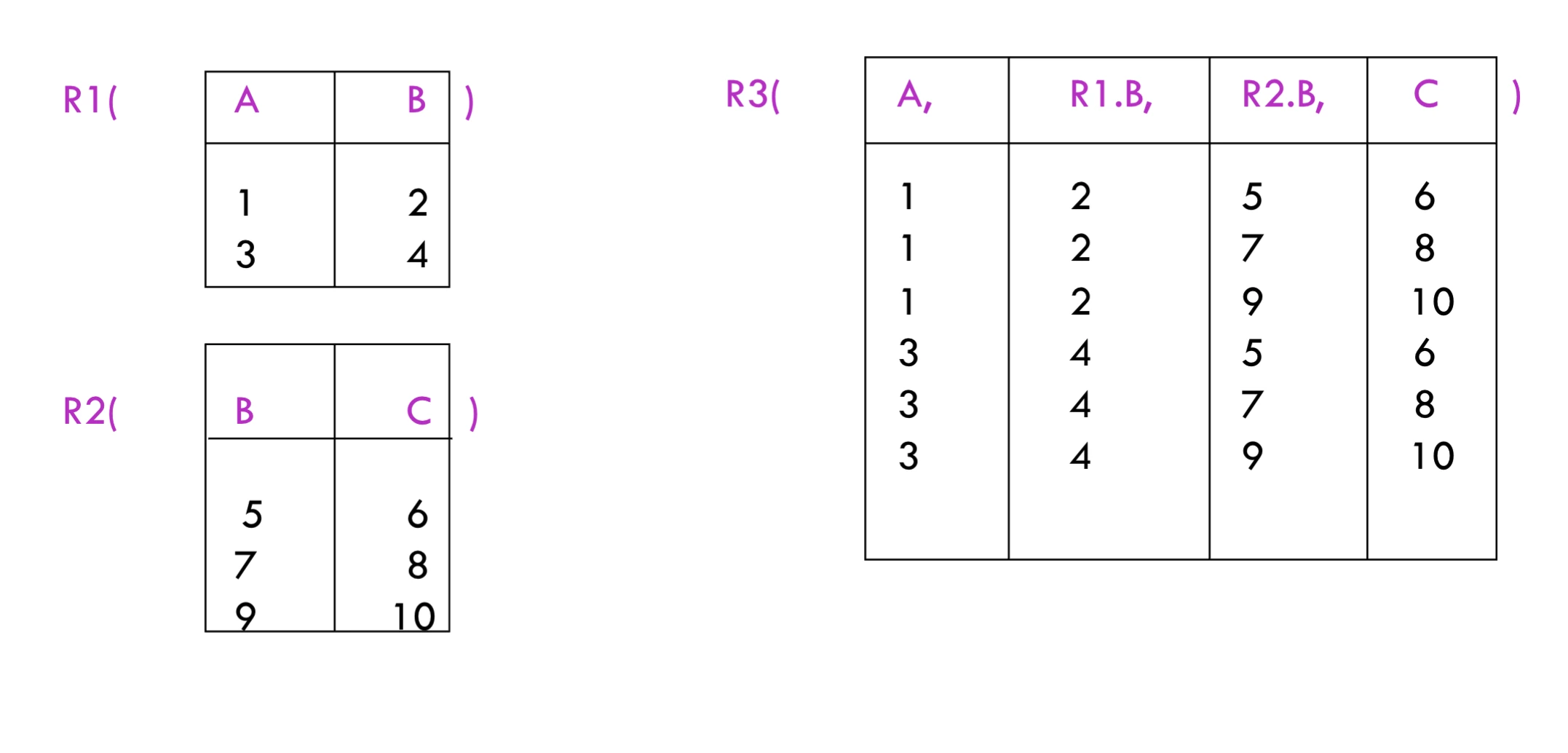
## theta-join

$$
R_{3} \coloneqq  R_{1} \bowtie_C R_{2}
$$

idea: product of $R_{1}$ and $R_{2}$ then apply $\sigma_C$ to results

think of $A \Theta B$ where $\Theta \coloneqq =, <, \text{ etc.}$

## natural join

$$
R_{3} \coloneqq  R_{1} \bowtie R_{2}
$$

- equating attributes of the same name
- projecting out one copy of each pair of equated attributes

![[thoughts/university/twenty-four-twenty-five/sfwr-3db3/natural-join.webp]]

## renaming

$$
R_{1} \coloneqq  \rho_{R_{1}(A_{1},\ldots,A_n)}(R_{2})
$$

## set operators

> \[!abstract\] union compatible
>
> two relations are said to be _union compatible_ if they have the same set of attributes and types (domain) of the attributes are the same

i.e: `Student(sNumber, sName)` and `Course(cNumber, cName)` are **not union compatible**

![[thoughts/bags]]

### Set Operations on Relations

For relations $R_1$ and $R_2$ that are union compatible, here’s how many times a tuple $t$ appears in the result:

| Operation    | Symbol       | Result (occurrences of tuple $t$) |
| ------------ | ------------ | --------------------------------- |
| Union        | $\cup$       | $m + n$                           |
| Intersection | $\cap$       | $\texttt{min}(m,n)$               |
| Difference   | $\textrm{-}$ | $\texttt{max}(0, m-n)$            |

where $m$ is the number of times $t$ appears in $R_1$ and $n$ is the number of times it appears in $R_2$.

### sequence of assignments

precedence of relational operators:

$$
\begin{aligned}
&\sigma \quad \pi \quad \rho \\[8pt]
& \times \quad \bowtie \\[9pt]
& \cap \\
&\cup \quad -
\end{aligned}
$$

### expression tree

![[thoughts/university/twenty-four-twenty-five/sfwr-3db3/expression-tree-relalg.webp]]

## extended algebra

$\delta$: eliminate duplication from bags

$\tau$: sort tuples

$\gamma_{L}(R)$ grouping and aggregation

outerjoin: avoid dangling tuples

### duplicate elimination

$$
\delta(R)
$$

Think of it as converting it to set

### sorting

$$
\tau_L(R)
$$

with $L$ is a list of some attributes of $R$

basically for ascending order, for descending order then use $\tau_{L, \text{DESC}}(R)$

### applying aggregation

or $\gamma_{L}(R)$

- group $R$ accordingly to all grouping attributes on $L$

- per group, compute `AGG(A)` for each aggrgation on $L$

- result has one tuple for each group: grouping attributes and aggregations

aggregation is applied to an entire column to produce a single results

### outerjoin

essentially padding missing attributes with `NULL`

## bag operations

> remember that bag and set operations are different

set union is idempotent, whereas bags union is not.rightarrow

bag union: $\{1,2,1\} \cup \{1,1,2,3,1\} = \{1,1,1,1,1,2,2,3\}$

bag intersection: $\{1,2,1,1\} \cap \{1,2,1,3\} = \{1,1,2\}$

bag difference: $\{1,2,1,1\} - \{1,2,3\} = \{1,1\}$