Root locus and graphical analysis

See also problem

Problemè 1

1.a

What does a root locus plot depict?

A root locus plot depicts locations of the closed-loop poles of a system in the complex $s$-plane as a function of a gain parameter, commonly the controller gain $K$

• represents how the roots (poles) of the closed-loop characteristic equation move in the complex plane is varied from $0 \to \infty$
• root locus starts at open-loop poles when $K=0$ and ends at open-loop zzeros when $K \to \infty$
• shape determines stability and transient response characteristics of the closed-loop system
• Points on root locus satisfy angle condition and magnitude condition in relation to the open-loop transfer function.

1.b

What must be done to a transfer function before its root locus can be graphed?

1. find the open-loop poles and zeros of $G(s)H(s)$, or solving $1+G(s)H(s)=0$. The poles are the roots of the denominator polynomial, and the zeros are the roots of the numerator polynomial.
2. determine the number of branches of the root locus, which is equal to the number of poles minus number of zeros
3. Check for root locus existence on the real axis.
4. Determine breakaway and break-in points where root locus departs from and arrives on the real axis, via solving $\frac{dK}{ds} = 0$, where K is the open-loop gain
5. Calculate asymptote centroid and angles. Centroid is the center of gravity of the poles and zeros. Asymptote angles are given by $(2q+1)*\frac{180}{P-Z}$ where $q=0,1,2,\dots$
6. Determine angle of departure and arrival at complex poles and zeros using angle condition.

1.c

What is the significance of the gain $K$?

K represents the variable loop gain in feedback control system. Since root locus starts at open-loop poles when $K=0$ and ends at open-loop zeros as $K \to \infty$, thus K determines the trajectory of closed-loop poles.

The stability and transient response characteristics of the closed-loop system depend on pole locations, which is determined by K. For example:

• If poles are in the right-half plane for a certain K, the system is unstable.
• Poles further from the origin (higher K) give faster response.
• Poles with larger imaginary parts (higher K) produce more oscillations.

Finally, K can be selected to achieve target spec like damping ratio, settling time, to shape system response via gain tuning

1.d

How can a root locus plot be used to design a controller?a\

1. Selecting K gain: root locus show trajectories of closed-loop poles as K varies. By selecting K, the desired pole locations can be achieved to meet the desired transient response characteristics.
2. Assessing stability: root locus allow determine range of K for which the closed-loop system is stable. System is stable if all poles lie in the left-half plane. Segments of the real axis to the left of an odd number of poles and zeros are part of the root locus.
3. Adding poles and zeros: If original root locus does not pass through the desired closed-loop pole locations, poles and zeros can be added via the controller to reshape the root locus (lead compensators add zeros and lag compensators add poles)
4. Meeting spec: Lines of constant damping ratio $\zeta$ and natural frequency $\omega_n$ can be drawn on the root locus to meet the desired transient response characteristics.
5. Improve steady-state error: Adding poles at the origin or close to it with PI or lag controllers increases the system types and reduces steady-state error.

1.e

Imagine we have a partially finished root locus plot where only the pole and zero locations have been plotted. What are the rules for completing the root locus plot using pencil and paper?

1. Number of branches:

   • Number of branches of the root locus is equal to the number of poles minus the number of zeros.
   • Branches start at poles and end at the zeros

2. Symmetry:

   • Root locus is symmetrical about the real axis

3. Real axis segments:

   • Portions of the real axis are part of the root locus if the number of real poles and zeros to the right is odd

4. Asymptotes as $K \to \infty$:

   • Asymptotes intersect at the centroid of the poles and zeros, and the angles are given by $(2q+1)*\frac{180}{P-Z}$ where $q=0,1,2,\dots$

5. Breakaway and break-in points:

   • Breakaway and break-in points where the locus departs from or arrives on the real axis can be found by solving for. They are found by solving $\frac{dK}{ds} = 0$.

---

Problemè 2

For each of the following transfer functions, sketch a root locus plot using the pencil-and-paper method you outlined above:

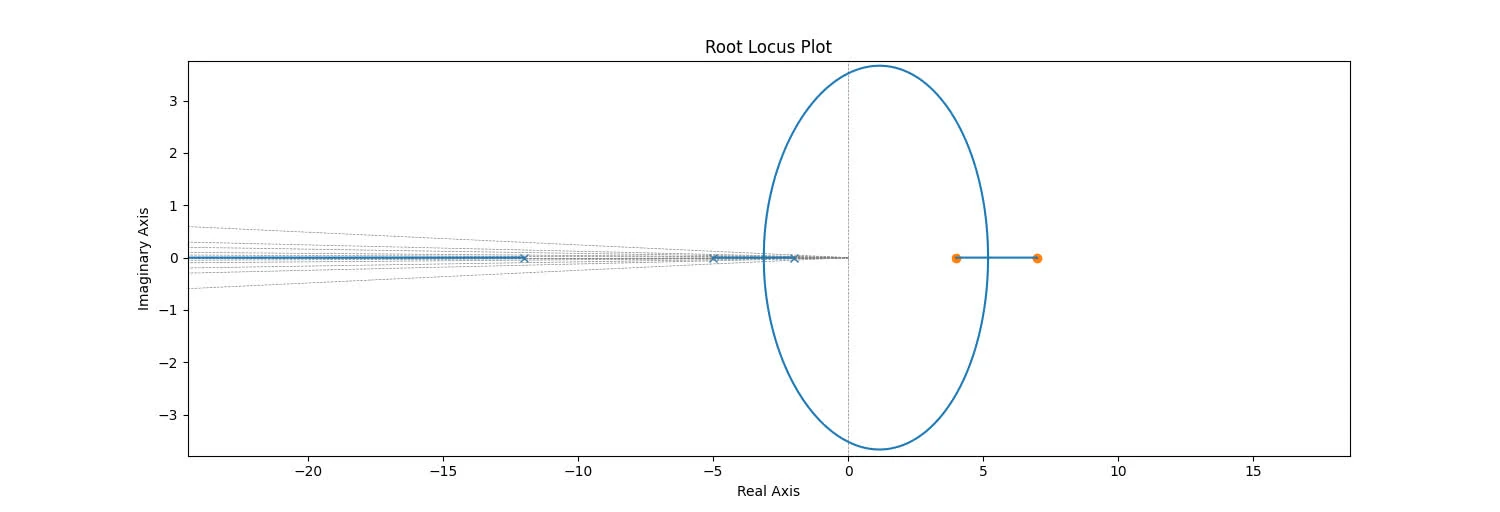
2.a

$$G(s) = \frac{1}{(s+5)(s+9)}$$

poles: $s=-5, -9, n=2$, zeros: $\infty, m=0$

branches: 2 ($n>m$)

asymptotes: $\theta = (2q+1)\frac{180}{(n-m)} = 90^\circ, 270^\circ$ for $q=0,1$

Centroid: $\omega = \frac{-5-9}{2} = -7$

root locus on real axis: exists to the left of -5 and -9

breakaway, angle of departure/arrival: not applicable since no complex zeros

locus is symmetrical about the real axis

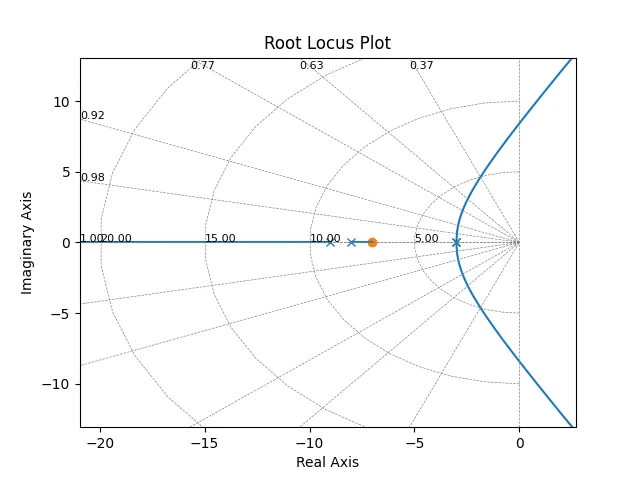
2.b

$$G(s) = \frac{(s-4)(s-7)}{(s+2)(s+5)(s+12)}$$

poles: $s=-2, -5, -12, n=3$, zeros: $s=4, 7, m=2$

branches: 3 ($n>m$)

asymptotes: $\theta = (2q+1)\frac{180}{(n-m)} = 180^\circ$ for $q=0$

centroid: $\omega = \frac{-2-5-12-4-7}{3-2} = -30$

root locus on real axis: on the axis from 7 to 4, and from -2 to -5, and from -12 to $-\infty$.

breakways/break-in points: solve for $s=\frac{dK}{ds}=0$, There are around two breakaways point, at $s=5.18, -3.13$

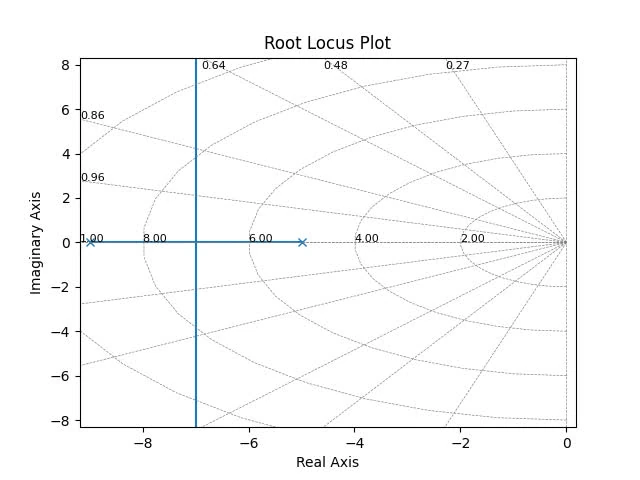
2.c

$$G(s) = \frac{(s+7)}{(s+8)(s+9)(s+3)^2}$$

poles: $s=-8, -9, -3, -3, n=4$, zeros: $s=-7, m=1$

branches: 4 ($n>m$)

asymptotes: $\theta = (2q+1)\frac{180}{(n-m)} = 120^\circ, 180^\circ, 300^\circ$ for $q=0,1,2$

centroid: $\omega = \frac{-8-9-3-3-7}{4-1} = -10$

root locus on real axis: on the axis from -3 to -3, and from -7 to -8, and from -9 to $-\infty$.

breakaways/break-in points: at $s=3$, which solves for $\frac{dK}{ds}=0$