see also RFC
The following document describes and summarises existing works in vLLM to improve general guided decoding performance.
requirements
- V1 Tensor Parallelism aware
- PR: vllm-project/vllm#9856
- Difference between TP in v0 and v1:
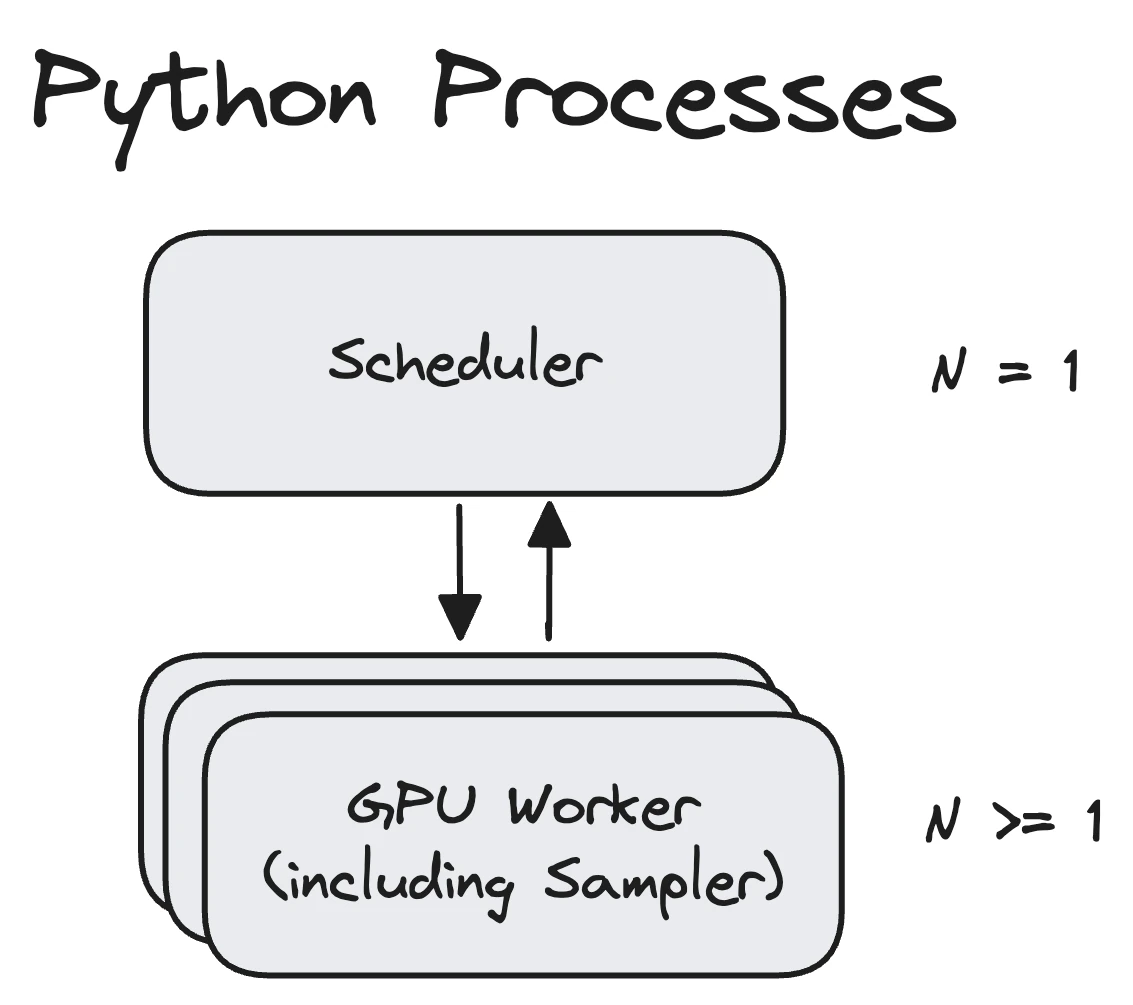
- The executor creates worker processes rather than processes
- All processes run
prepare_inputs. - All processes run the sampler. In other word, all workers REQUIRE result logits such that
logits_processorcan performall_gatherinstead of localgatherops. - The executor broadcasts the scheduler output to the workers and one of them sends back the model runner output — both of these IPCs use shared memory message queues.
- The workers sit in a very tight model execution loop where they only handle model execution and process termination.
- performance over features/alternative backends
- Right way versus flexibility of backends
- We will choose the fastest backends.
proposal
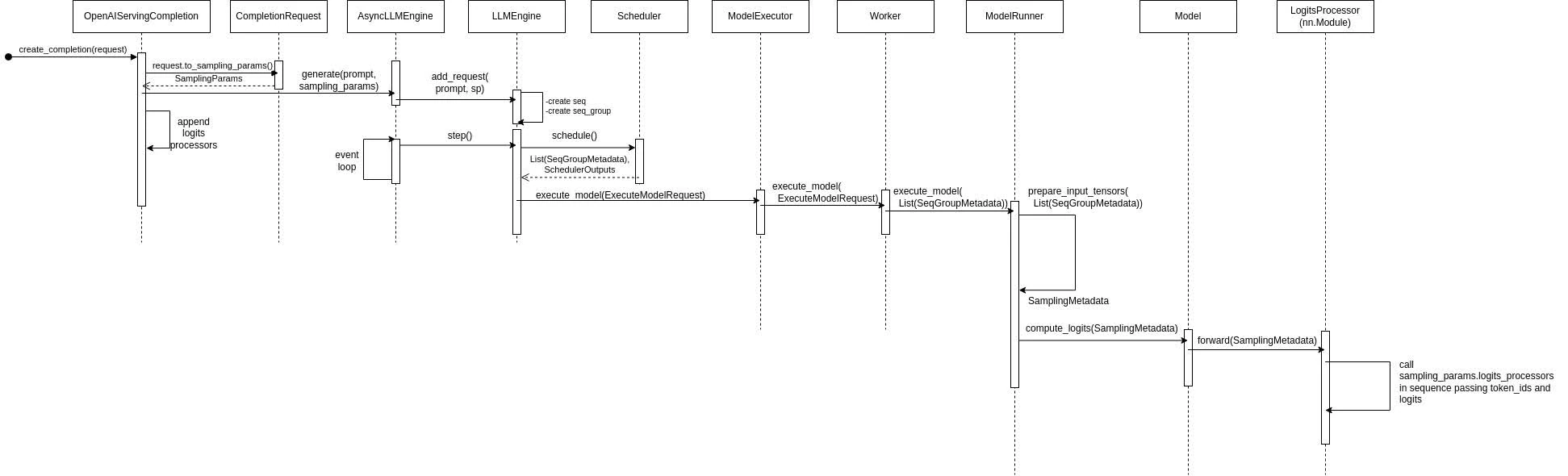
Components of structured decoding will be split into two components:
- Scheduler:
- request-aware for which guided decoding requests (in a sense it won’t block other requests in the same batch, from motivation
- Add the guided requests to a “waiting” queue, mark them as
UNREADY, and the scheduler will skip those requests until FSM is ready. This means all requests will have higher priority once FSM is ready- think of the waiting queue as a
deque - Better TTFT
- think of the waiting queue as a
- Advance the FSM after sampler output is received from workers and broadcast updated bitmask from the FSM to GPU workers
- Note that this can be parallel to the next forward pass occurring on the workers
- Requires two broadcast
- (P1) Jump-forward decoding support (backtrack versus advance accordingly)
- Worker:
- Apply the logit bias from bitmask received from the scheduler.
alternatives consideration
The following were rejected from WG meeting:
- Logit Processor Abstraction
- We need more information at the scheduler-level for future proof
background
reference: vllm-project/vllm#5329
Currently, generations with FSM is super slow, even with warmup steps to initialize given FSM. This behaviour is further exemplified when running with context longer than 4096 tokens.
Additionally, all outlines logit processors are considered stateful, which slows down the model executor, given in V0 logit processors are applied row-by-row blocking
Thus comparing to sglang, vLLM v0 is currently not up to par.
Doesn’t have jump-ahead decoding with logit processor approach.
@cadedaniel: “tree scoring in [spec decode] could use the same API as multi-path jump decoding.”
How should we handle FSM per requests?
- Currently, users can specify different schemas per request, which means the FSM will be compiled per request. This is suboptimal because it slows down general TTFT.
- For most use cases, we should assume JSON schema similar to how the system prompt is currently being handled (pass during server init)
Why should we follow the plugins system?
- If going with the best options, then what is the reasoning behind supporting different backends?
- Agree for extensibility, but seems to add additional overhead.
appendix.
The following includes background information about guided generations.
batched constrained decoding using pushdown automaton
Implemented in mlc-ai/xgrammar
Quote
calculate adaptive token bit-mask per batch
IMPORTANT
operating on string level, not
token_id
GrammarMatcher ⇒ FSM in xgrammar
questions
- byte-level automaton
overhead of token_id ⇒ string
Token for context-independent tokens vs dependent tokens within the generation masks
async pre-compile
synchronize apply mask for CPU → GPU?
How do we apply said masks to GPU block? Zero-overhead generations?
worst-case scenario for grammar compilation?
mask gen overhead: 36
time linearly increase for batch size?
parallelize for compilation.
do we need to parallelize on vLLM?
no, xgrammar parallelize it, with
pthread
shape of masks?
bitmask, tensors of vocab size ⇒ concat with recast ⇒ GPU
supported tokenizers?
GLM yet to be supported (Nov 22nd)
Given that detokenizer is in a separate process with vLLM, then can we stops duplicating this process?
Currently with
xgrammar: detokenizer included in mask generations.token_id ⇒ tokens
future plans
- Function calling support
- Support more grammar (CFG, Python grammar)
compressed FSM for jump-ahead tokens.
Implemented in (Zheng et al., 2024)
Method 1: FSM-based decoding
-
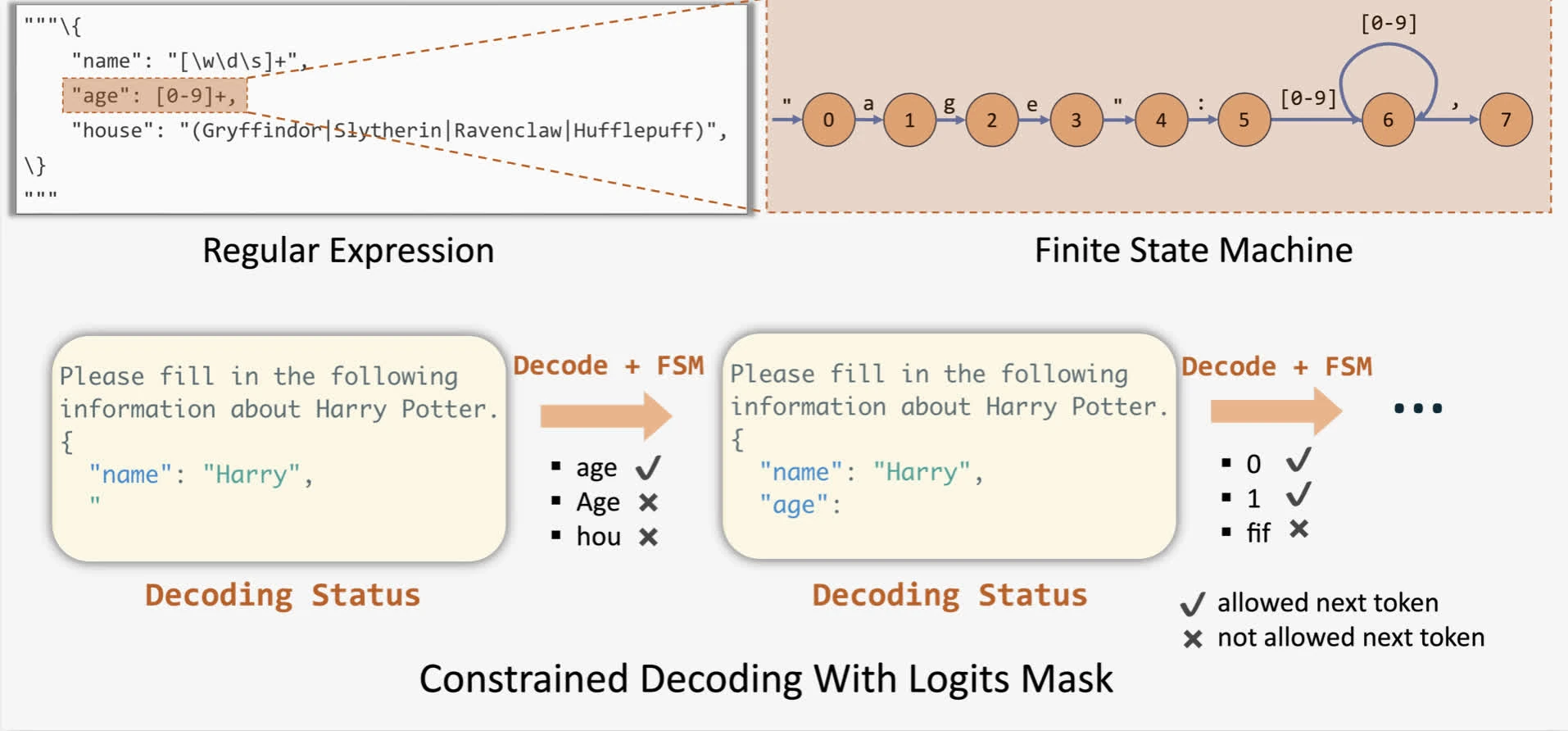
intuition: Using FSM (Willard & Louf, 2023) to guide generations by increasing logit bias for tokens that conform to given JSON schema. This allows us to track the current state during decoding and filter out invalid tokens by applying logit bias to the output.
-
limitation: we can see that given construction of FSM requires token-level access, it can only transition the state by only one token at a time, resulting in slow decoding.
Method 2: Interleaved-based
-
intuition: breaks down JSON schemas, each containing either a chunk prefill part or constrained decoding part. They are then executed interleaved by inference system. Faster than per-token decoding given that chunked prefill components can process multiple tokens per forward pass
See also https://github.com/guidance-ai/guidance#guidance-acceleration using llama.cpp as backend.
-
limitation:
- interleaved-based require custom syntax, making it less expressive compared to regex.
- struggles to deal with tokenization boundaries due to conflicts between decode and chunked prefill segments.
- frequent communications between interpreter and back-end adds additional overhead.
Method 3: Jump-Forward Decoding with compressed FSM
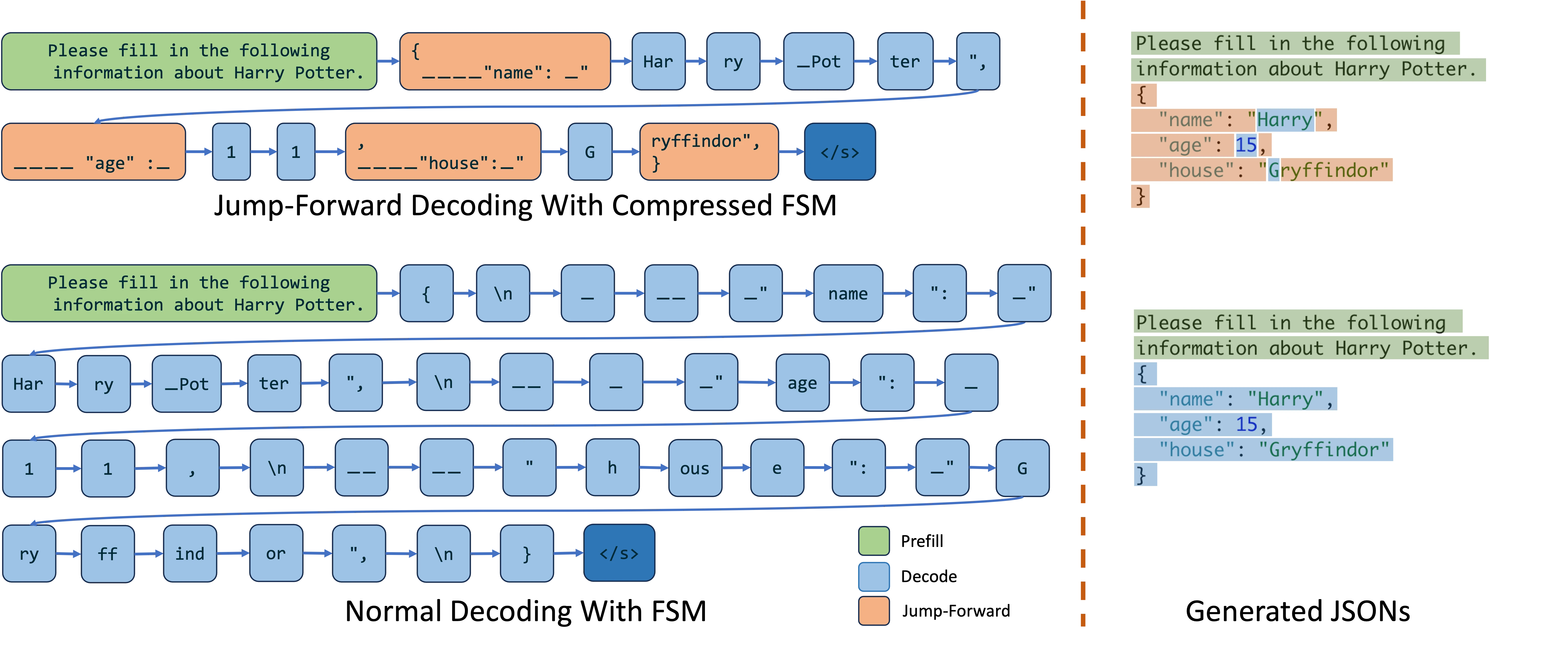
tokenization boundary handling
During decoding, it is preferred to combine multiple characters into a single tokens.
For example, when decoding
"Hello"in context of JSON decoding, LLM might output the following token",He,llo,",This may cause some strange behaviour if we combine the last
"with,(this regex"[\w\d\s]*"with the last,will lead to endless decoding because this token",is not valid even if the LM wants to stop.)
Fix:
- implement re-tokenization mechanism during jump-forward phase (append string instead of the tokens, followed with re-tokenization of the entire text) add approximately 4% of overhead
- use a comprehensive regex to guide the decoding phase, instead of employing multiple concatenated regex 1
Coalescence
intuition: Instead of expanding to state, we can compress certain chunks into one state to reduce the size of said FSM.
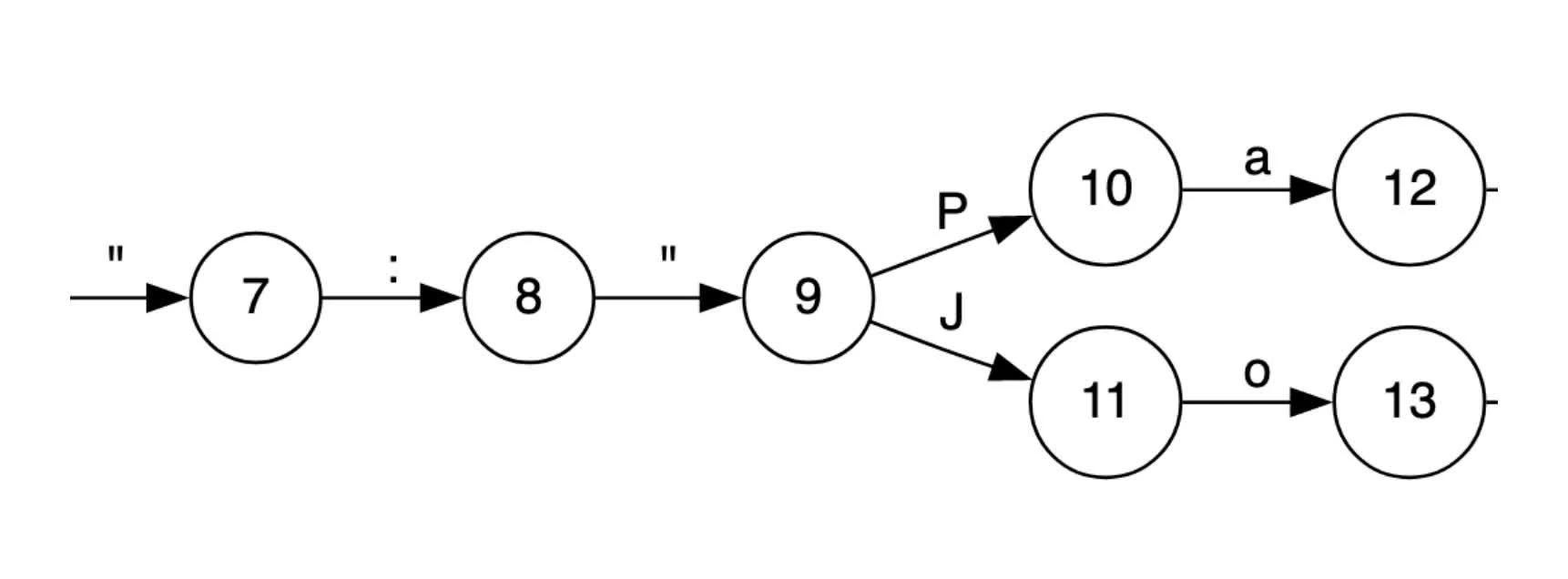 figure 1: initial FSM state
figure 1: initial FSM state
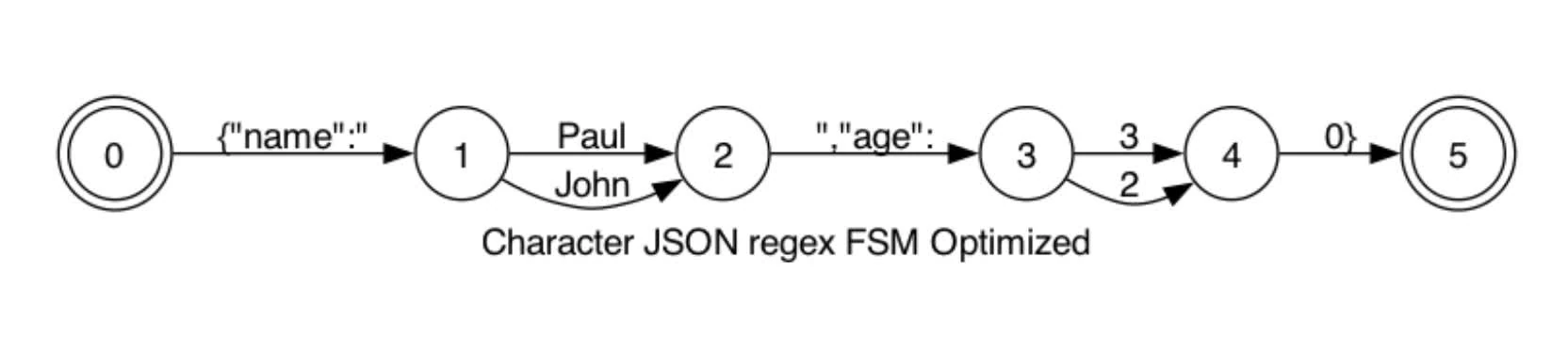 figure 2: compressed FSM state
figure 2: compressed FSM state
A way to adapt character regex to work with tokens in outlines:
import outlines.fsm as fsm
from outlines.fsm.regex import make_deterministic_fsm, create_fsm_index_tokenizer
new_fsm, _ = make_deterministic_fsm(fsm)
idx, _ = create_fsm_index_tokenizer(new_fsm, tokenizer)stateDiagram-v2 [*] --> InputPrompt: Start state "input prompt" as InputPrompt state "next-token probability distribution" as GetProb state "valid tokens" as ListTokens { [*] --> CheckTransitions CheckTransitions --> FilterTokens: Get index[0].keys() FilterTokens --> [*] } state "Sample Token" as SampleToken state "Update FSM State" as UpdateState InputPrompt --> GetProb: "model.generate" GetProb --> ListTokens: Get next-token distribution ListTokens --> SampleToken: Use filtered token list SampleToken --> UpdateState: Selected token X UpdateState --> [*]: new_state = index[0]["X"]
idx_with_tokens = {
state: {tokenizer.tokenizer.decode([key]): value for key, value in transitions.items()}
for state, transitions in idx.items()
}example
stateDiagram-v2 direction LR 0 --> 2: n 0 --> 1: t 1 --> 2: a 2 --> 4: na 2 --> 3: a 3 --> 5: am 4 --> 6: me 5 --> 6: me 2 --> 6: name 6 --> 7: e 6 --> 8: c 7 --> 9: p 8 --> 9: p 9 --> 11: Paul 9 --> 12: Pa 9 --> 10: Jo 11 --> 13: aul 12 --> 14: ul 10 --> 26: o 26 --> 27: h 27 --> 14: n 13 --> 14: l 14 --> 16: s 14 --> 15: s 15 --> 17: s 16 --> 17: s 17 --> 18: a 17 --> 19: ag 18 --> 20: ge 19 --> 20: e 20 --> 21: 30 20 --> 22: 20 21 --> 24: 2 22 --> 24: 2 22 --> 23: 3 24 --> 25: 0 25 --> [*]
note: each state of FSM represents a forward pass to the LM. In vanilla generation, this is essentially necessary. Thus there is no added overhead of FSM for controlling the generated outputs.
From state 2-6, we observer that there are eight different paths to get the same generations of name. We probably don’t need to do this, given that it will all give us result name
But suffice to say, we can hijack this behaviour to accelerate generations by append either of the following tokens word to currently generated sequence:
- [”name”]
- [”n”, “a”, “m”, “e”]
- [”na”, “m”, “e”]
- [”nam”, “e”]
- [”n”, “am”, “e”]
- [”n”, “ame”]
- [”na”, “me”]
- [”n”, “a”, “me”]
A simplified index can be shown as:
simplified_index = {
0: {'{"': 2},
2: {"name": 6},
6: {'":"': 9},
9: {'Paul': 14, 'John': 14},
14: {'","': 17},
17: {'age': 20},
20: {'":': 22},
22: {'20': 24, '30': 24},
24: {'}': 25},
}That’s at least a 5x speedup over structured generations, given that out of the 9 tokens, two states are single-state transitions. Therefore we only need to call the model twice!!
difference in sampling distribution
All these paths lead to the same string and the same speedup, however they lead to potentially very different states for the LLM when it reaches state 6. That is, the strings are the same, but each path leads to a different conditional probability distribution in stage 6.

Guided generations with FSM.
(Willard & Louf, 2023), implemented at https://github.com/dottxt-ai/outlines
assumption: we are building against autoregressive transformers models
- Let , where is the power set operator, be subset of multi-token string that ends with tokens .
- Text generation tasks is to draw samples from
Notable sampling methods include greedy decoding (generate tokens recursively with highest probability tokens), beam search (but using heuristic to find the mode of distribution) 2
A pseudocode for sampling procedure is as follow:
Algorithm 4 LLM token sampling
1:function sample()
2:
3:for do
4:
5:Sample
6:if then
7:break
8:end if
9:
10:end for
11:
12:return
13:end function
Given that we are dealing with finite discrete distribution, we can then compute an un-normalized conditional distribution by applying a boolean mask , which restricts the support of original distribution:
augmentation upon sampling algorithm
Algorithm 5 token sampling with masking
1:function sample()
2:
3:for do
4:
5:Construct the mask m()
6:
7:Sample
8:if then
9:break
10:end if
11:
12:end for
13:
14:return
15:end function
finite automaton
We define a finite-state machine, given by 3 where character comprising the strings in are drawn from , i.e:
> FSM making for regular expression
([0-9]*)?\.?[0-9]*example illustration
For simplicity, let the vocabulary consists of strings
- generations start: FSM in state 0, so it masks “A”, since it wouldn’t accepted by the FSM. Then we only sample ”.”, “42”, “.2”, “1” in this case
- if we sample “.2” then we advance the FSM to state 3. In this case. only “42” and “1” are valid completions, so we mask other values before sampling. If we sample “1” instead, then we advance FSM to state 1, in which case ”.”, “.42”, “.2”, and “1” are valid completions
determinism
Looping through the vocabulary is still the biggest issue. For that, we preprocess the vocabulary using Regex’s FSM and build a index. Thus a proceeding for producing matches starting at any point in the FSM is required.
We define finding sub-sequences of FSM that accept string as follow:
Algorithm 6 Find sub-sequences of the FSM that accept the string
1:function FindSubSequences()
2:
3:
4:for do ▷
5:
6:for do ▷
7:if then ▷
8:
9:break ▷
10:end if
11:
12:
13:end for
14:
15:end for
16:
17:return
18:end function
We can then define construction of
Algorithm 7 Construct a map from FSM states to subsets of
1:function MapStatesToVocab()
2:
3:Initialize the map with empty sets for each element in
4:for do ▷
5:
6:for do ▷
7:
8:end for
9:end for
10:
11:return
12:end function
Bibliographie
- Lew, A. K., Zhi-Xuan, T., Grand, G., & Mansinghka, V. K. (2023). Sequential Monte Carlo Steering of Large Language Models using Probabilistic Programs. arXiv preprint arXiv:2306.03081 [arXiv]

- Willard, B. T., & Louf, R. (2023). Efficient Guided Generation for Large Language Models. arXiv preprint arXiv:2307.09702 [arXiv]

- Zheng, L., Yin, L., Xie, Z., Sun, C., Huang, J., Yu, C. H., Cao, S., Kozyrakis, C., Stoica, I., Gonzalez, J. E., Barrett, C., & Sheng, Y. (2024). SGLang: Efficient Execution of Structured Language Model Programs. arXiv preprint arXiv:2312.07104 [arXiv]

Remarque
-
this phenomena is also known as coalescence in structured generations, where it exploit deterministic structures in desired outputs to skip expensive forward pass ↩
-
(Lew et al., 2023) recently proposes a sequential Monte Carlo steering. The idea is to classify causal generations as a posteriori inference problem in a class of discrete probabilistic sequence models.
See also Feynman-Kac transformers models ↩
-
- is a finite set of states
- is a finite alphabet
- is the transition function
- is the start state
- is the set of all accepted states.