see also pdf (Cybenko, 1989)

idea: a single sigmoid activation functions in FFN can approximate closely any given probability distributions.

Think of just a linear layers with some activation functions

import torch.optim as optim
import torch.nn as nn
 
class LinearRegression(nn.Module):
  def __init__(self, input_dim, output_dim):
    super().__init__()
    self.fc = nn.Linear(input_dim, output_dim)
  def forward(self, x): return self.fc(x)
 
model = LinearRegression(224, 10)
loss = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=0.005)
 
for ep in range(10):
  y_pred = model(X)
  l = loss(Y, y_pred)
  l.backward()
  optimizer.setp()
  optimzer.zero_grad()

Think of one-hot encoding (binary or multiclass) cases

context: using SGD we can compute the gradient:

This is expensive, given that for deep model this is repetitive!

intuition: we want to minimize the error and optimized the saved weights learned through one forward pass.

happens in deeper network wrt the partial derivatives

because we applies the chain rule and propagating error signals backward from the output layer through all the hidden layers to the input, in very deep networks, this involves successive multiplication of gradients from each layer.

thus the saturated neurons $\sigma^{'}(x) \approx 0$, thus gradient does not reach the first layers.

solution:

• we can probably use activation functions (Leaky ReLU)
• better initialisation
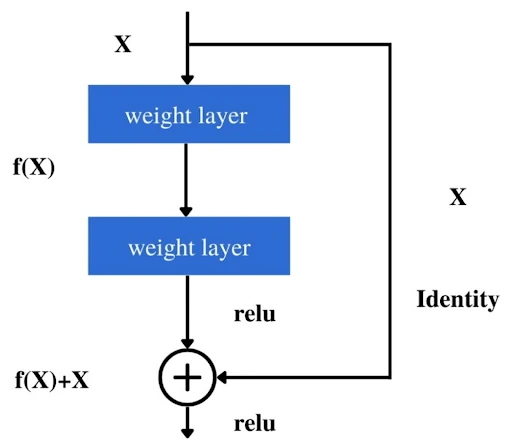
• residual network

• url: thoughts/regularization

regularization

usually prone to overfitting given they are often over-parameterized

1. We can usually add regularization terms to the objective functions
2. Early stopping
3. Adding noise
4. structural regularization, via adding dropout

dropout

a case of structural regularization

a technique of randomly drop each node with probability $p$

Lien vers l'original