---
date: '2024-12-18'
description: think of Laplace transform, but for sampled data
id: Z-transform
modified: 2026-06-05 15:08:26 GMT-04:00
tags:
  - math
  - sfwr4aa4
  - sfwr3dx4
title: Z-transform
created: '2024-12-18'
published: '2024-12-18'
pageLayout: default
slug: thoughts/Z-transform
permalink: https://aarnphm.xyz/thoughts/Z-transform.md
generator:
  quartz: v4.6.0
  hostedProvider: Cloudflare
  baseUrl: aarnphm.xyz
full: https://aarnphm.xyz/llms-full.txt
---
reference: [[thoughts/university/twenty-four-twenty-five/sfwr-4aa4/lec/17_z-trans_practice.pdf|examples for z-transform]]

| **Sequence**    | **Transform**                                    |
| --------------- | ------------------------------------------------ |
| $\delta(k - n)$ | $z^{-n}$                                         |
| $1$             | $\frac{z}{z - 1}$                                |
| $k$             | $\frac{z}{(z - 1)^2}$                            |
| $k^2$           | $\frac{z(z + 1)}{(z - 1)^3}$                     |
| $a^k$           | $\frac{z}{z - a}$                                |
| $ka^k$          | $\frac{az}{(z - a)^2}$                           |
| $\sin ak$       | $\frac{z \sin a}{z^2 - 2z \cos a + 1}$           |
| $\cos ak$       | $\frac{z(z - \cos a)}{z^2 - 2z \cos a + 1}$      |
| $a^k \sin bk$   | $\frac{az \sin b}{z^2 - 2az \cos b + a^2}$       |
| $a^k \cos bk$   | $\frac{z^2 - az \cos b}{z^2 - 2az \cos b + a^2}$ |

## properties

**Linearity**: if $x(n) = af_{1}(n) + bf_{2}(n)$ then $X(z) = aF_{1}(z) + bF_{2}(z)$

**Time shifting**:

$$
\begin{aligned}
Z[x(t)] &= X(z) \\
x(k-n) &= z^{-n}X(z) \\
x(k+n) &= z^{n}X(z)
\end{aligned}
$$

## [[thoughts/quantization]] error

> \[!note\] sampling
>
> The idea to convert analog to digital

$T$ is the sampling period, and $\frac{1}{T}$ is the sampling rate in _cycles per second_

$$
\text{error} = \frac{M}{2^{n+1}}
$$

where $n$ is number of bits used for digitalisation

> \[!note\] resolution of A/D converter
>
> minimum value of the output that can be represented as binary number, or $\frac{M}{2^n}$

## sampled data system

reference input $r$ is the sequence of sample values $r(kT)$

A **sampler** is a switch that closes every $T$ seconds:

$$
r^{*}(t) = \sum_{k=0}^{\infty} r(kT) \delta (t-kT) \quad (t>0)
$$

Transfer function of sampled data:

$$
R^{*}(s) = \mathcal{L} (r^{*}(t)) = \sum_{k=0}^{\infty} r(kT) e^{-ksT}
$$

## definition

Let $z = e^{sT}$, we have the following definition:

> \[!definition\] Definition 1. z-transform
>
> $$
> Z \{r(t)\}  = F(z) = Z(r^{*}(t)) = \sum_{k=0}^{\infty} r(kT)z^{-k}
> $$

## zero-order hold

Transfer function of Zero-Order hold

$$
\mathcal{L}(u(t) - u(t-T)) = \frac{1}{s} - \frac{e^{sT}}{s}
$$

## finding the discrete transfer function

$G(s) = \frac{s^2 + 4s + 3}{s^3 + 6s^2 + 8s}$

$$
\begin{aligned}
G(s) &= \frac{s^2 + 4s + 3}{s^3 + 6s^2 + 8s} = \frac{0.375}{s} + \frac{0.25}{s+2} + \frac{0.375}{s+4} \\
G(t) &= \mathcal{L}^{-1}(G(s)) = 0.375 + 0.25 e^{-2t} + 0.375 e^{-4t} \\
G(z) &= Z(G(t)) = 0.375 \frac{z}{z-1} + 0.25 \frac{z}{z-e^{-2T}} + 0.375 \frac{z}{z-e^{-4T}}
\end{aligned}
$$

## inverse z-transform

$G(z) \to x(k)$

### power series

_use: when G(z) is expressed as the ratio of two polynomials in z_

$$
G(z) = a_{0} + a_{1} z^{-1} + a_{2} z^{-2} + \ldots
$$

### partial fraction

For example: $G(z) = \frac{z}{(z-1)(z-2)} = \frac{-z}{z-1} + \frac{z}{z-2} = \sum_{k=0}^{\infty} (-1 + 2^k)z^{-k}$

thus, $g(kT) = 2^k-1$

## stability

| system            | pole location criteria on z-plane                                    |
| ----------------- | -------------------------------------------------------------------- |
| Stable            | All poles inside unit circle                                         |
| Unstable          | Any poles outside unit circle                                        |
| Marginally Stable | One or more poles on unit circle, remaining poles inside unit circle |

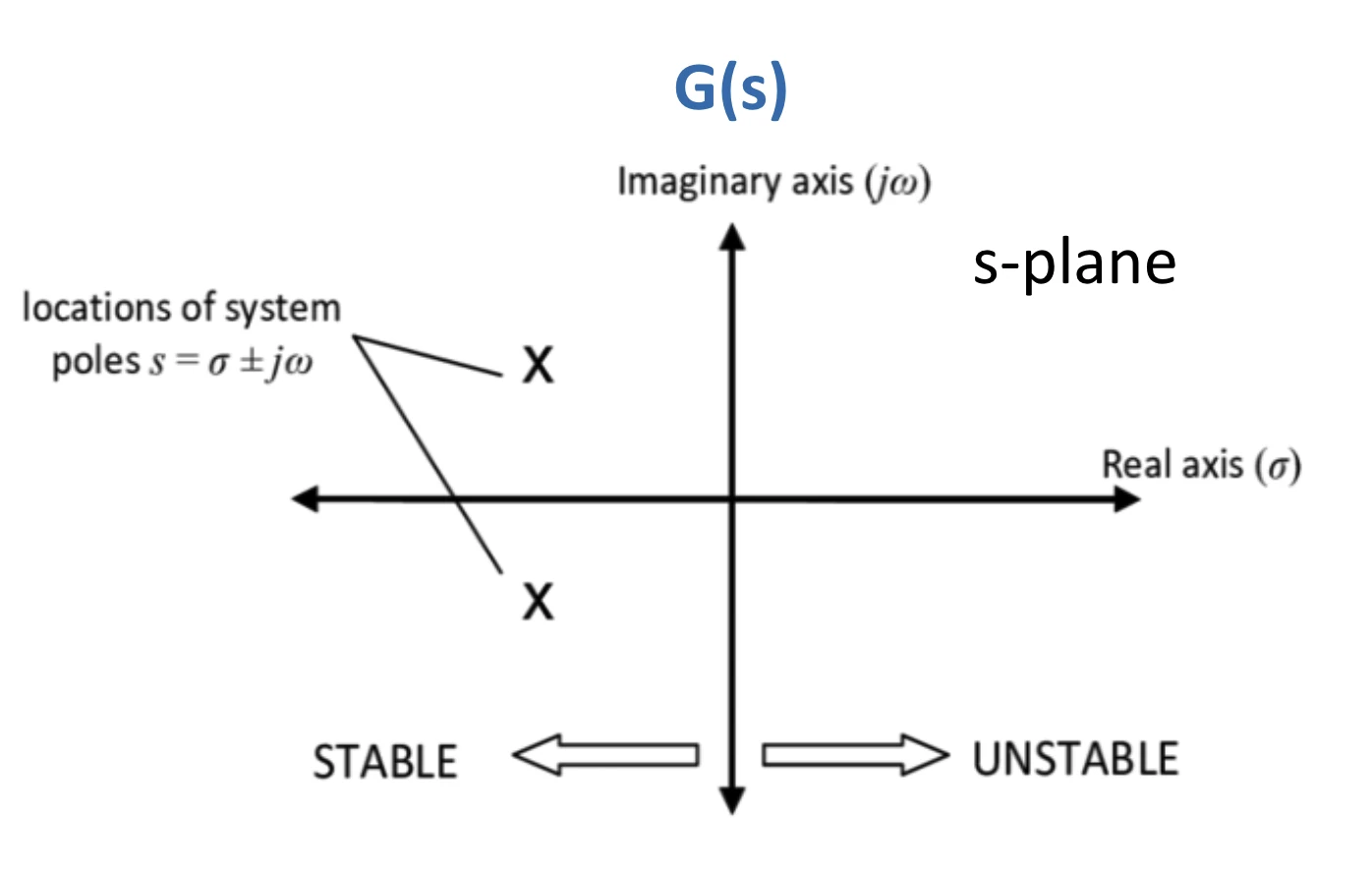![[thoughts/university/twenty-four-twenty-five/sfwr-4aa4/s-plane-stability.webp|poles on s-plane]]

> \[!tip\] mapping from s-plane to z-plane
>
> $$
> z = e^{\alpha T}(\cos \omega T + j \sin \omega T)
> $$

### we assume $s = \alpha + j \omega$

| Location on s-plane        | Value of $\alpha$ | Value of $e^{\alpha T}$ | Mapping on z-plane  |
| -------------------------- | ----------------- | ----------------------- | ------------------- |
| Imaginary axis ($j\omega$) | $\alpha = 0$      | $e^{\alpha T} = 1$      | On unit circle      |
| Right half-plane           | $\alpha > 0$      | $e^{\alpha T} > 1$      | Outside unit circle |
| Left half-plane            | $\alpha < 0$      | $e^{\alpha T} < 1$      | Inside unit circle  |

## final value theorem

> \[!abstract\] definition
>
> If $\lim_{k \to \infty}x(k)$ exists, then the follow exists:
>
> $$
> \lim_{k \to \infty} x(k) = \lim_{z \to 1} (z-1) X(z)
> $$

## [[thoughts/Root locus|root locus]] on z-plane

- derive open loop function $K \bar{GH}$
- Factor numerator and denominator to get open loop zeros and poles
- Plot roots of $1+K \bar{GH}=0$ in z-plane as k varies
  $\bar{GH(z)} = \frac{N(z)}{D(z)}$