profile
⌘ '
raccourcis clavier
Search

Quantization

  • Étiquette

    • publié à

    • modifié à

    • durée

      2 min de lecture (334 words)

    • source

      llms.txt

    See also: this talk I gave at Hack the North 2023.

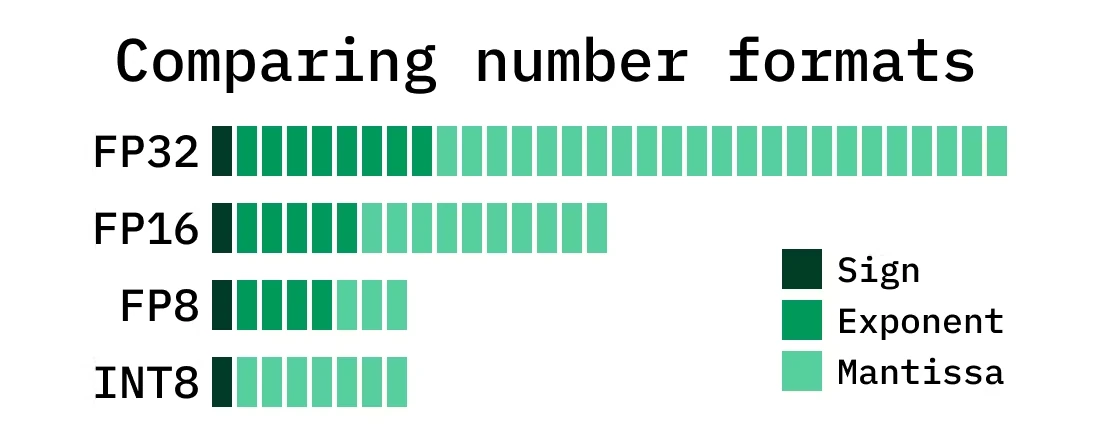
    reduce computational and memory costs of running inference with representing the weight and activations with low-precision data type

    Note

    This also applies to post-training quantization, where the methodology is applied after the model has been trained, instead of during load-time.

    from baseten introduction into quantization format
    from baseten introduction into quantization format

    metrics for calibration

    the idea is to compare the difference between two probability distribution when scaling, for example from int16 to int8

    KL calibration

    fp32 to fp16

    Does my operation support fp16?

    • CPU does support saving fp16 weights, but computations are done in fp32

    Does my operation sensitive to fp16?

    For example epsilon in LayerNormalization usually is very small 1e−121e^{-12}, but smallest value in fp16 is ≈6e−5\approx 6e^{-5}, which cause NaN issues.

    fp32 to int8

    Consider a float x in [a, b], such that affine quantization scheme:

    x=S⋅(xq−Z)x = S \cdot (x_q - Z)

    where:

    • xqx_q is the quantized int8 associated with x
    • SS and ZZ are scaling and zero-point parameters
      • SS is the scale, positive float32
      • ZZ is the zero-point, or the int8 value corresponding to value 0 in fp32

    Thus quantized value xqx_q is: xq=round(x/S+Z)x_q = \text{round}(x / S + Z)

    And fp32 value outside of [a, b] is clipped to closest representable value.

    ∀x∈[a,b]xq=clip(round(x/S+Z),round(a/S+Z),round(b/S+Z))\forall x \in [a, b] \quad x_q = \text{clip}(\text{round}(x/S + Z), \text{round}(a/S + Z), \text{round}(b/S + Z))

    See also: paperarXiv

    quantization time

    • Post-training dynamic quantization: range of each activation is computed on the fly at runtime
    • Post-training static quantization: range of each activation is computed offline before runtime
      • Observers are put on activations to collect their value
      • certain number of forward passes on calibration datasets
      • range of each computation are computed according to some calibration technique
    • Quantization aware training: range of each activation is computed during training
      • fake_quantize operations are inserted in the computation graph
      • fake_quantize is a no-op during inference, but during training, it simulates the effect of quantization

    Methods and libraries

    bitsandbytes and GPTQarXiv

    Vous pourriez aimer ce qui suit

  • Prompt engineering
  • aesthetic value
  • Metaphysics
  • Radix tree
  • Epistemology
  • Behavirourism
  • being.
    • LLMs
    large language models, often implemented as autoregressive transformers models. GPTs and friends Most variants of LLMs are decoder-only (Radford et al., 2019) Have “capabilities” to understand natural language.
    Z-transform
    think of Laplace transform, but for sampled data
    craft.
    and celebration of the act of making.
    Quantization
    See also: this talk I gave at Hack the North 2023. reduce computational and memory costs of running inference with representing the weight and activations with low-precision data type int16 - half precision bfloat16 int8 fp8 Note This also applies to post-training quantization, where the methodology is applied after the model has been trained, instead of during load-time.