---
date: '2024-12-18'
description: z-transform analysis of discrete-time control systems with zero-order hold, block diagram reduction, and transfer functions.
id: closed loop system
modified: 2026-06-05 15:08:42 GMT-04:00
tags:
  - sfwr4aa4
title: closed loop system
created: '2024-12-18'
published: '2024-12-18'
pageLayout: default
slug: thoughts/university/twenty-four-twenty-five/sfwr-4aa4/closed-loop-system
permalink: https://aarnphm.xyz/thoughts/university/twenty-four-twenty-five/sfwr-4aa4/closed-loop-system.md
generator:
  quartz: v4.6.0
  hostedProvider: Cloudflare
  baseUrl: aarnphm.xyz
full: https://aarnphm.xyz/llms-full.txt
---
For determine discrete systems and vice versa.

## $G(z)$ with a Zero-Order hold

$$
G(z) = (1-z^{-1}) Z[\frac{G_p(s)}{s}] = G^{*}(z) - z^{-1}G^{*}(z)
$$

example: Find $G(z)$ if $G_p(s) = \frac{s+2}{s+1}$

$$
\begin{aligned}
G^{*}(s) &= \frac{G_p(s)}{s} = \frac{2}{s} - \frac{1}{s+1} \\[8pt]
g^{*}(t) &= 2 - e^{-t} \quad (\text{inverse Laplace transform}) \\
g^{*}(kT) &= 2 - e^{-kT} \\
G^{*}(z) = \frac{2z}{z-1} - \frac{z}{z-e^{-T}}
\end{aligned}
$$

## block diagram reduction

![[thoughts/university/twenty-four-twenty-five/sfwr-4aa4/closed-loop-z-block-diagram-reduction.webp]]

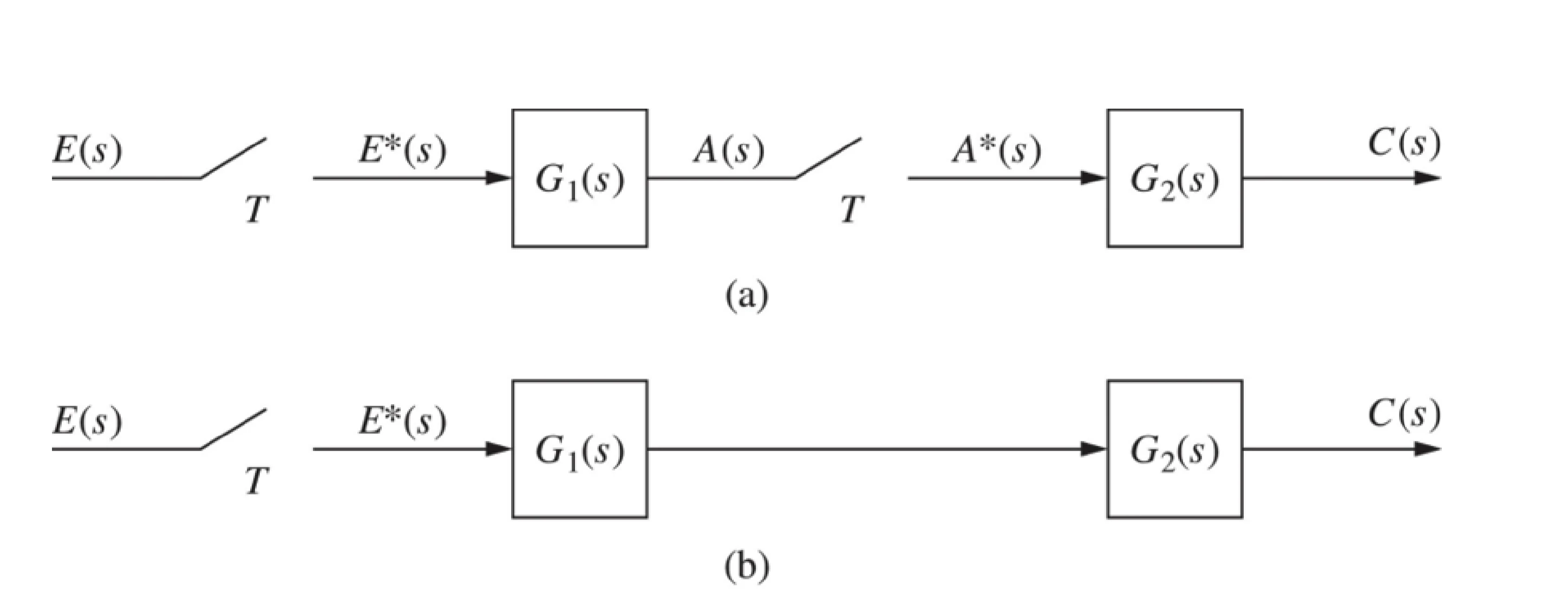
a. $C(z) = G_1(z) G_2(z) E(z)$
b. $C(z) = Z[G_1(s) G_2(s)]E(z)$

> \[!note\] Note
>
> The product of $G_1(s)G_2(s)$ must be evaluated first

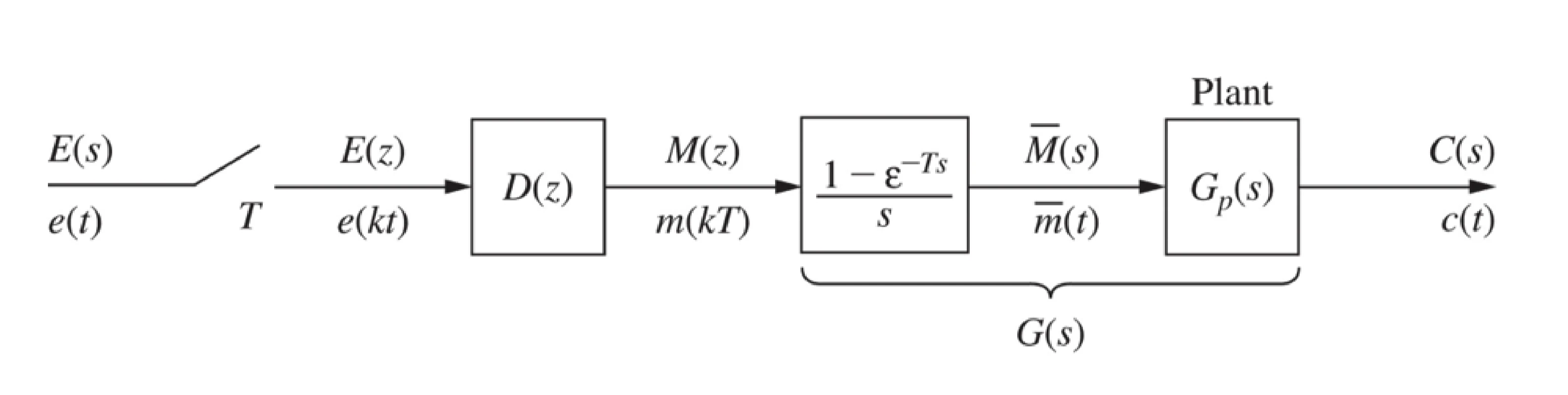
## model for Open-loop system

The output of open-loop system is

$$
C(z) = G(z)D(z)E(z)
$$

![[thoughts/university/twenty-four-twenty-five/sfwr-4aa4/model-open-loop-system.webp]]

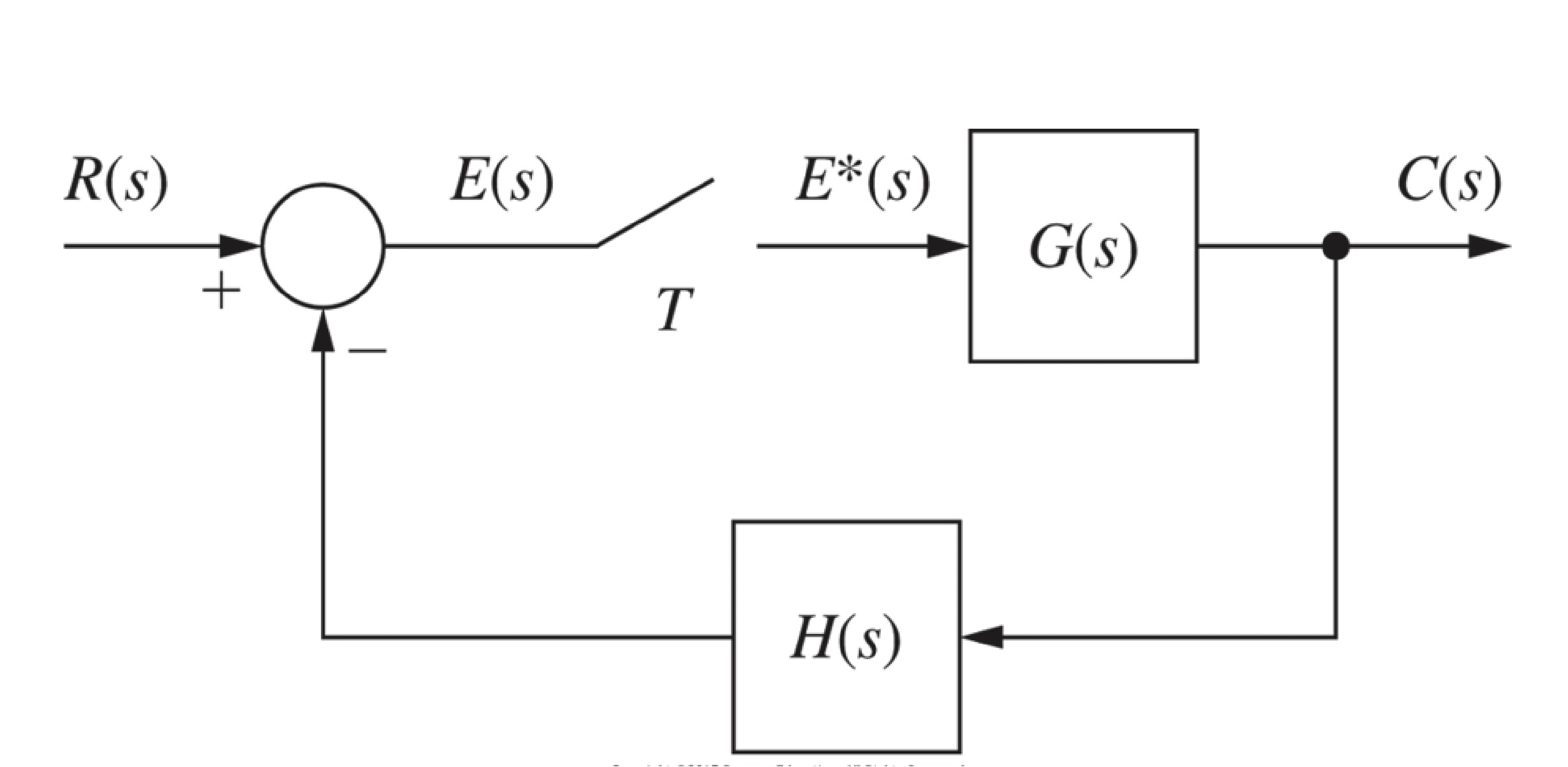
## closed loop sample data system

$$
\begin{aligned}
E(z) &= R(z) - Z[G(s)H(s)]E(z) \\[12pt]
&\because \frac{C(z)}{R(z)} = \frac{G(z)}{1+Z[G(s)H(s)]}
\end{aligned}
$$

![[thoughts/university/twenty-four-twenty-five/sfwr-4aa4/closed-loop-sampled-data-system.webp]]

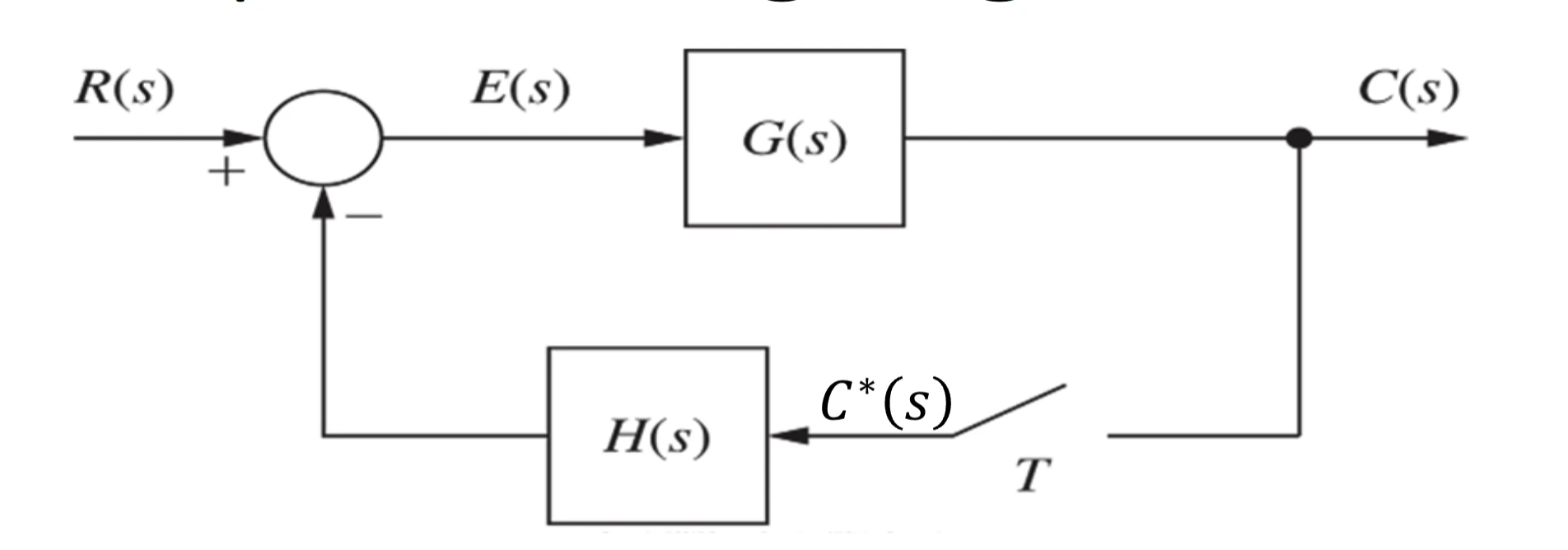
### using digital sensing device

$$
C(z) = \frac{Z[G(s)R(s)]}{1+Z(G(s)H(s))}
$$

![[thoughts/university/twenty-four-twenty-five/sfwr-4aa4/closed-loop-tf-sensing-device.webp]]

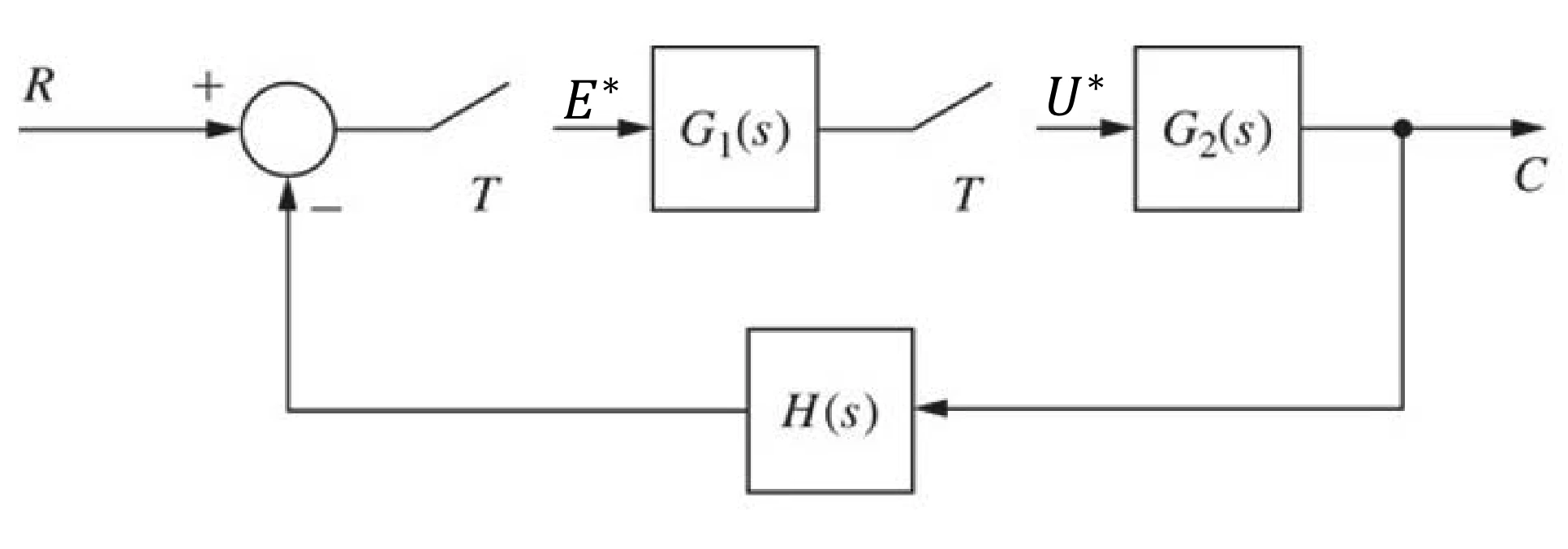
### using digital controller

$$
\frac{C(z)}{R(z)} = \frac{G_{1}(z)G_{1}(z)}{1+G_{1}(z)Z(G_{2}(s)H(s))}
$$

![[thoughts/university/twenty-four-twenty-five/sfwr-4aa4/closed-loop-tf-digital-controller.webp]]

## time response

$$
T(z) = \frac{G(z)}{1+G(z)}
$$