sparse autoencoder

abbrev: SAE

see also: landspace

Often contains one layers of MLP with few linear ReLU that is trained on a subset of datasets the main LLMs is trained on.

empirical example: if we wish to interpret all features related to the author Camus, we might want to train an SAEs based on all given text of Camus to interpret “similar” features from Llama-3.1

definition

We wish to decompose a models’ activitation $x \in \mathbb{R}^n$ into sparse, linear combination of feature directions:

$$\begin{aligned} x \sim x_{0} + &\sum_{i=1}^{M} f_i(x) d_i \\[8pt] \because \quad &d_i M \gg n:\text{ latent unit-norm feature direction} \\ &f_i(x) \ge 0: \text{ corresponding feature activation for }x \end{aligned}$$

Thus, the baseline architecture of SAEs is a linear autoencoder with L1 penalty on the activations:

$$\begin{aligned} f(x) &\coloneqq \text{ReLU}(W_\text{enc}(x - b_\text{dec}) + b_\text{enc}) \\ \hat{x}(f) &\coloneqq W_\text{dec} f(x) + b_\text{dec} \end{aligned}$$

training it to reconstruct a large dataset of model activations $x \sim \mathcal{D}$, constraining hidden representation $f$ to be sparse

L1 norm with coefficient $\lambda$ to construct loss during training:

$$\begin{aligned} \mathcal{L}(x) &\coloneqq \| x-\hat{x}(f(x)) \|_2^2 + \lambda \| f(x) \|_1 \\[8pt] &\because \|x-\hat{x}(f(x)) \|_2^2 : \text{ reconstruction loss} \end{aligned}$$

intuition

We need to reconstruction fidelity at a given sparsity level, as measured by L0 via a mixture of reconstruction fidelity and L1 regularization.

We can reduce sparsity loss term without affecting reconstruction by scaling up norm of decoder weights, or constraining norms of columns $W_\text{dec}$ during training

Ideas: output of decoder $f(x)$ has two roles

• detects what features acre active ⇐ L1 is crucial to ensure sparsity in decomposition
• estimates magnitudes of active features ⇐ L1 is unwanted bias

Gated SAE

uses Pareto improvement over training to reduce L1 penalty (Rajamanoharan et al., 2024)

Clear consequence of the bias during training is shrinkage (Sharkey, 2024) ¹

Idea is to use gated ReLU encoder (Dauphin et al., 2017; Shazeer, 2020):

$$\tilde{f}(\mathbf{x}) \coloneqq \underbrace{\mathbb{1}[\underbrace{(\mathbf{W}_{\text{gate}}(\mathbf{x} - \mathbf{b}_{\text{dec}}) + \mathbf{b}_{\text{gate}}) > 0}_{\pi_{\text{gate}}(\mathbf{x})}]}_{f_{\text{gate}}(\mathbf{x})} \odot \underbrace{\text{ReLU}(\mathbf{W}_{\text{mag}}(\mathbf{x} - \mathbf{b}_{\text{dec}}) + \mathbf{b}_{\text{mag}})}_{f_{\text{mag}}(\mathbf{x})}$$

where $\mathbb{1}[\bullet > 0]$ is the (point-wise) Heaviside step function and $\odot$ denotes element-wise multiplication.

term	annotations
$f_\text{gate}$	which features are deemed to be active
$f_\text{mag}$	feature activation magnitudes (for features that have been deemed to be active)
$\pi_\text{gate}(x)$	$f_\text{gate}$ sub-layer’s pre-activations

to negate the increases in parameters, use weight sharing:

Scale $W_\text{mag}$ in terms of $W_\text{gate}$ with a vector-valued rescaling parameter $r_\text{mag} \in \mathbb{R}^M$:

$$(W_\text{mag})_{ij} \coloneqq (\exp (r_\text{mag}))_i \cdot (W_\text{gate})_{ij}$$

Figure 3: Gated SAE with weight sharing between gating and magnitude paths

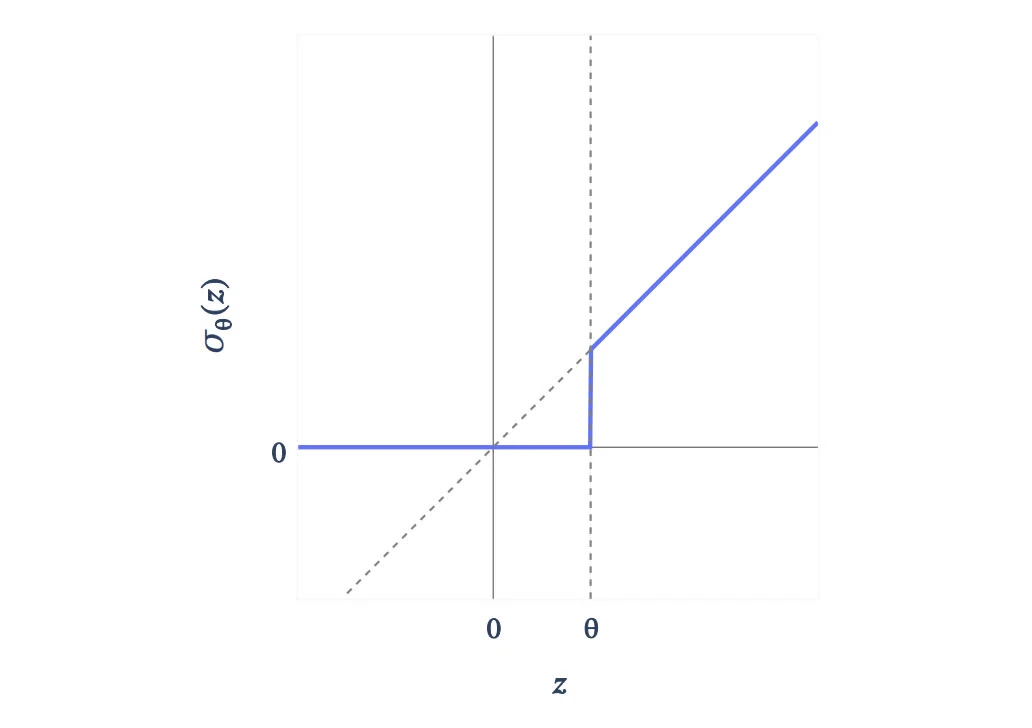
Figure 4: A gated encoder become a single layer linear encoder with Jump ReLU (Erichson et al., 2019) activation function $\sigma_\theta$

feature suppression

See also: link

Loss function of SAEs combines a MSE reconstruction loss with sparsity term:

$$\begin{aligned} L(x, f(x), y) &= \|y-x\|^2/d + c\mid f(x) \mid \\[8pt] &\because d: \text{ dimensionality of }x \end{aligned}$$

the reconstruction is not perfect, given that only one is reconstruction. For smaller value of $f(x)$, features will be suppressed

illustrated example

consider one binary feature in one dimension $x=1$ with probability $p$ and $x=0$ otherwise. Ideally, optimal SAE would extract feature activation of $f(x) \in \{0,1\}$ and have decoder $W_d=1$

However, if we train SAE optimizing loss function $L(x, f(x), y)$, let say encoder outputs feature activation $a$ if $x=1$ and 0 otherwise, ignore bias term, the optimization problem becomes:

$$\begin{aligned} a &= \argmin p * L(1,a,a) + (1-p) * L(0,0,0) \\ &= \argmin (1-a)^2 + \mid a \mid * c \\ &= \argmin a^2 + (c-2) *a +1 \end{aligned} \Longrightarrow \boxed{a = 1-\frac{c}{2}}$$

How do we fix feature suppression in training SAEs?

introduce element-wise scaling factor per feature in-between encoder and decoder, represented by vector $s$:

$$\begin{aligned} f(x) &= \text{ReLU}(W_e x + b_e) \\ f_s(x) &= s \odot f(x) \\ y &= W_d f_s(x) + b_d \end{aligned}$$

References

• Dauphin, Y. N., Fan, A., Auli, M., & Grangier, D. (2017). Language Modeling with Gated Convolutional Networks. arXiv preprint arXiv:1612.08083 arxiv
• Erichson, N. B., Yao, Z., & Mahoney, M. W. (2019). JumpReLU: A Retrofit Defense Strategy for Adversarial Attacks. arXiv preprint arXiv:1904.03750 arxiv
• Rajamanoharan, S., Conmy, A., Smith, L., Lieberum, T., Varma, V., Kramár, J., Shah, R., & Nanda, N. (2024). Improving Dictionary Learning with Gated Sparse Autoencoders. arXiv preprint arXiv:2404.16014 arxiv
• Sharkey, L. (2024). Addressing Feature Suppression in SAEs. AI Alignment Forum. [post]
• Shazeer, N. (2020). GLU Variants Improve Transformer. arXiv preprint arXiv:2002.05202 arxiv

Footnotes

1. If we hold $\hat{x}(\bullet)$ fixed, thus L1 pushes $f(x) \to 0$, while reconstruction loss pushes $f(x)$ high enough to produce accurate reconstruction.

   An optimal value is somewhere between.

   However, rescaling the shrink feature activations (Sharkey, 2024) is not necessarily enough to overcome bias induced by L1: a SAE might learnt sub-optimal encoder and decoder directions that is not improved by the fixed. ↩