--- date: '2024-12-16' description: analysis of first-order and second-order system responses, time constants, and rise time calculations. id: system response modified: 2026-06-05 15:08:43 GMT-04:00 tags: - sfwr4aa4 title: System response created: '2024-12-16' published: '2024-12-16' pageLayout: default slug: thoughts/university/twenty-four-twenty-five/sfwr-4aa4/system-response permalink: https://aarnphm.xyz/thoughts/university/twenty-four-twenty-five/sfwr-4aa4/system-response.md generator: quartz: v4.6.0 hostedProvider: Cloudflare baseUrl: aarnphm.xyz full: https://aarnphm.xyz/llms-full.txt --- We will consider first-order and second-order system ## 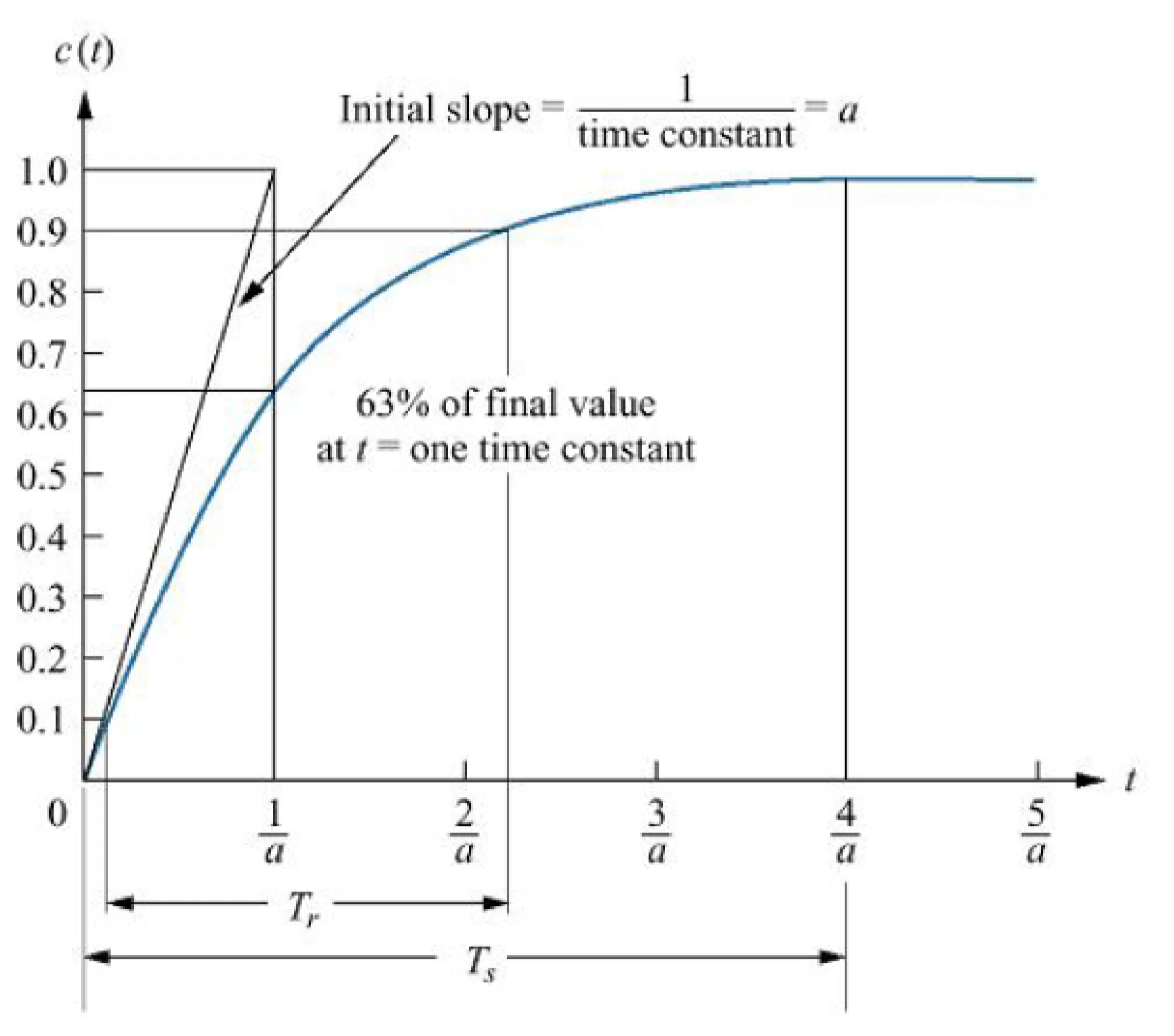first-order systems, time constant
"\\usepackage{tikz}\n\\usetikzlibrary{positioning}\n\n\\begin{document}\n\\begin{tikzpicture}[auto, node distance=2cm, >=latex]\n\n% Nodes\n\\node[draw, rectangle, minimum width=3cm, minimum height=1.5cm] (block) {$\\frac{a}{s + a}$};\n\\node[left=1.5cm of block] (input) {$X(s) = \\frac{1}{s}$};\n\\node[right=1.5cm of block] (output) {$Y(s)$};\n\\node[above=0.5cm of block] (G) {$G(s)$};\n\n% Arrows\n\\draw[->] (input) -- (block);\n\\draw[->] (block) -- (output);\n\n\\end{tikzpicture}\n\\end{document}"tikz diagram
source code
Output of a general first-order system is $$ Y(s) = X(s)G(s) = \frac{a}{s(s+a)} $$ thus the time domain output is $y(t) = 1 - e^{-at}$ > \[!tip\] time constant > > usually, $t=\frac{1}{a}$, and $y(t) = 0.63$, hence 63.2% to find the rise time. ### response in time domain > \[!abstract\] rise time `T_r` > > $T_r$, time for the waveform to go from 0.1 to 0.8 of its final value > > for first order: $T_r = \frac{2.2}{a}$ > \[!abstract\] settling time `T_s` > > $T_s$, time for response to reach and stay with 2% of its final value > > for first order: $T_s = \frac{4}{a}$ ![[thoughts/university/twenty-four-twenty-five/sfwr-4aa4/time-response-freq-domain.webp]] ## second-order systems general order system: $$ G(s) = \frac{b}{s^{2}+as +b} $$ Thus the pole for this system: $$ s_{1},s_{2}= \frac{-a + \sqrt{a^2 - 4b}}{2} $$ ### natural frequency _happens when $a=0$_ The transfer function is $G(s)=\frac{b}{s^{2}+b}$, and poles will only have imaginary $\pm jw$ > $w_n = \sqrt{b}$ is the frequency of oscillation of this system. in a sense, this is the undamped case: ![[thoughts/university/twenty-four-twenty-five/sfwr-4aa4/undamped-natural-freq.webp]] ### damping coefficient complex poles has real part $\sigma = -\frac{a}{2}$ > \[!definition\] Definition 1. 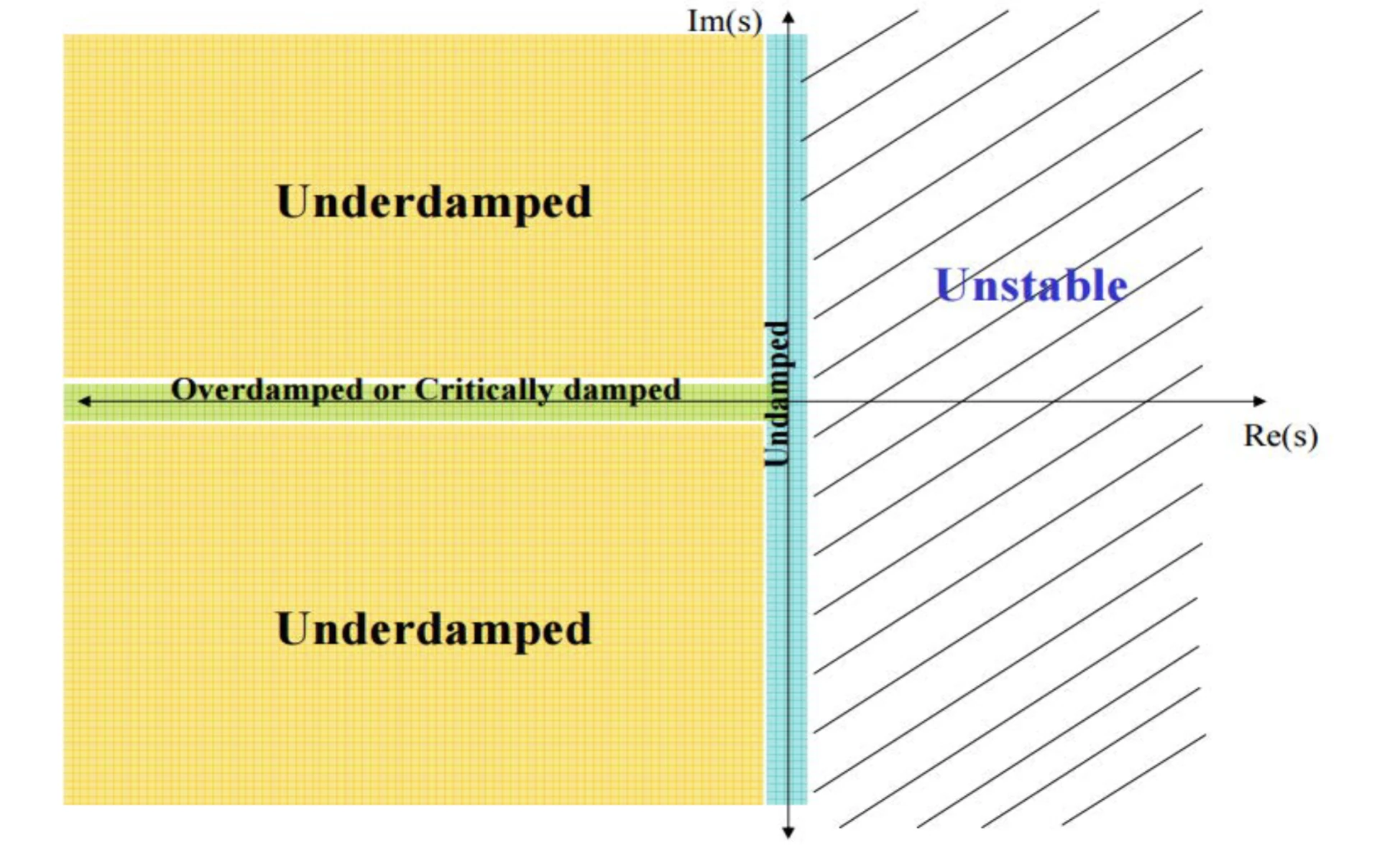> > damping ratio is defined as: > > $$ > \zeta = \frac{\text{exponential decay frequency}}{\text{natural frequency}} = \frac{|\sigma|}{w_n} > $$ So that $a = 2 \zeta w_n$ ### general second order $$ \begin{aligned} G(s) &= \frac{w_n^2}{s^2 + 2 \zeta w_n s + w_n^2} \\[12pt] s_{1},s_{2} &= - \zeta w_n \pm w_n \sqrt{\zeta^2 - 1} \end{aligned} $$ ### observations | Condition | Poles | pole type | Damping Ratio ($\zeta$) | Natural Response $c(t)$ | | ----------------- | ------------------------- | --------- | ----------------------- | ------------------------------------------------------------------------------------ | | Undamped | $\pm j \omega_n$ | imaginary | $\zeta = 0$ | $A \cos (\omega_n t - \varphi)$ | | Underdamped | $\omega_d \pm j \omega_d$ | complex | $0 < \zeta < 1$ | $A e^{(-\sigma_d)t} \cos (\omega_d t - \varphi)$ where $w_d = w_n \sqrt{1- \zeta^2}$ | | critically damped | $\sigma_1$ | real | $\zeta = 1$ | $K t e^{\sigma_1 t}$ | | overdamped | $\sigma_1 \quad \sigma_2$ | real | $\zeta > 1$ | $K (e^{\sigma_1 t} + e^{\sigma_2 t})$ | ![[thoughts/university/twenty-four-twenty-five/sfwr-4aa4/sec-order-impulse-response.webp]] ### underdamped second-order step response Transfer function $C(s)$ is given by $$ C(s) = \frac{w_n^2}{s(s^2 + 2 \zeta w_n s + w_n^2)} $$ response in time-domain via inverse Laplace transform: $$ c(t) = 1 - \frac{1}{\sqrt{1- \zeta^2}} e^{- \zeta w_n t} \cos (\sqrt{1- \zeta^2}\omega_n t + \varphi) $$ where $\varphi = \tan^{-1} (\frac{\zeta}{\sqrt{1-\zeta^2}})$ ![[thoughts/university/twenty-four-twenty-five/sfwr-4aa4/peak-graph-time-response.webp]] ### 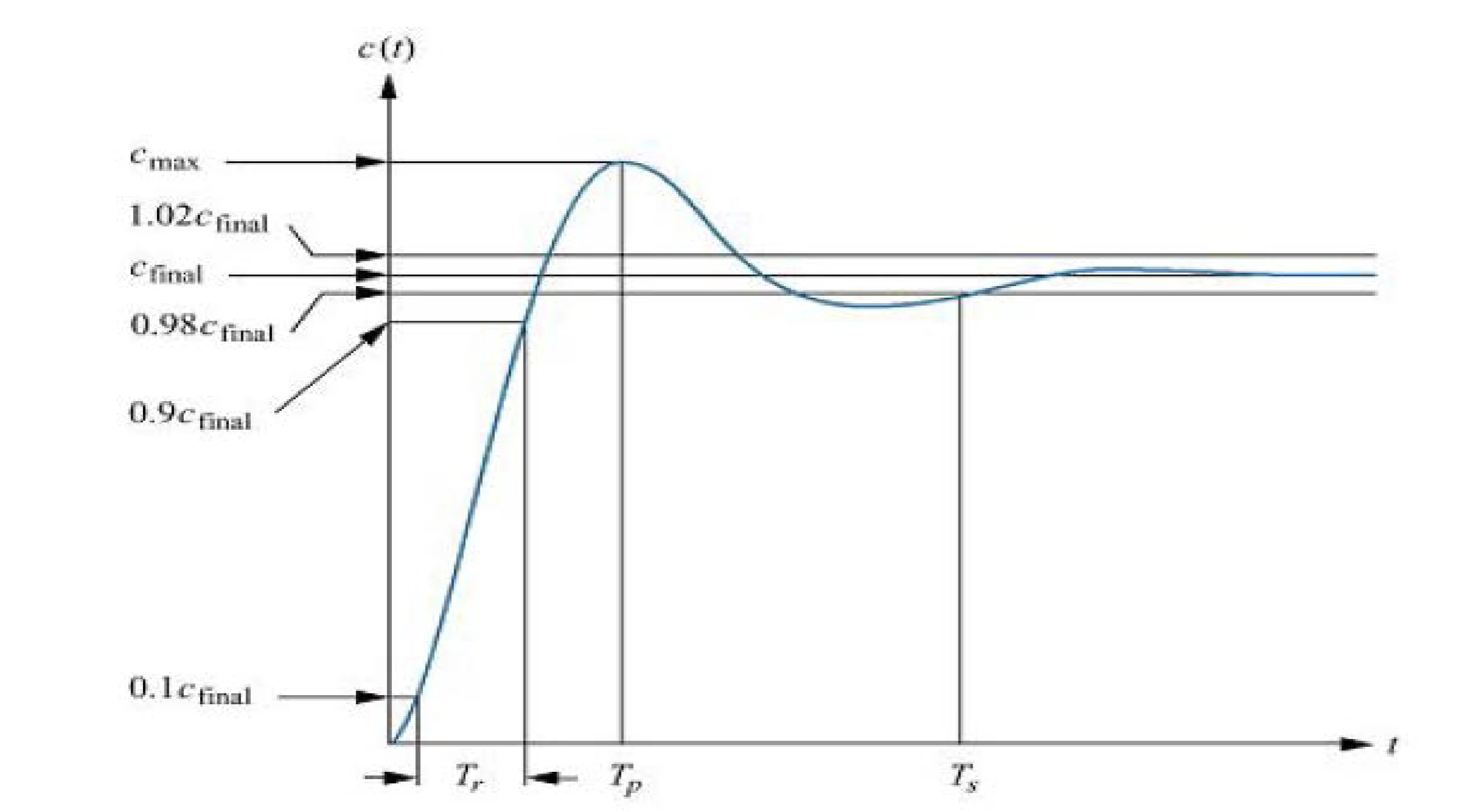peak time $T_p$ _time required to reach the first or maximum peak_ $$ T_p = \frac{\pi}{\omega_n \sqrt{1-\zeta^2}} $$ ### percent overshoot ![[thoughts/university/twenty-three-twenty-four/sfwr-3dx4/Time response#%OS (percent overshoot)|percent overshoot]] or in terms of damping ratio $\zeta$: $$ \zeta = \frac{-\ln \frac{\text{\%OS}}{100}}{\sqrt{\pi^2 + \ln^2(\frac{\text{\%OS}}{100})}} $$ ### relations to poles $$ \begin{aligned} G(s) &= \frac{w_n^2}{s^2 + 2 \zeta w_n s + w_n^2} \\[12pt] s_{1},s_{2} &= - \zeta w_n \pm w_n \sqrt{\zeta^2 - 1} \\[8pt] T_p &= \frac{\pi}{\omega_n \sqrt{1-\zeta^2}} \\ T_s &\cong \frac{4}{\zeta \omega_n} \end{aligned} $$ ![[thoughts/university/twenty-four-twenty-five/sfwr-4aa4/relations-to-poles.webp|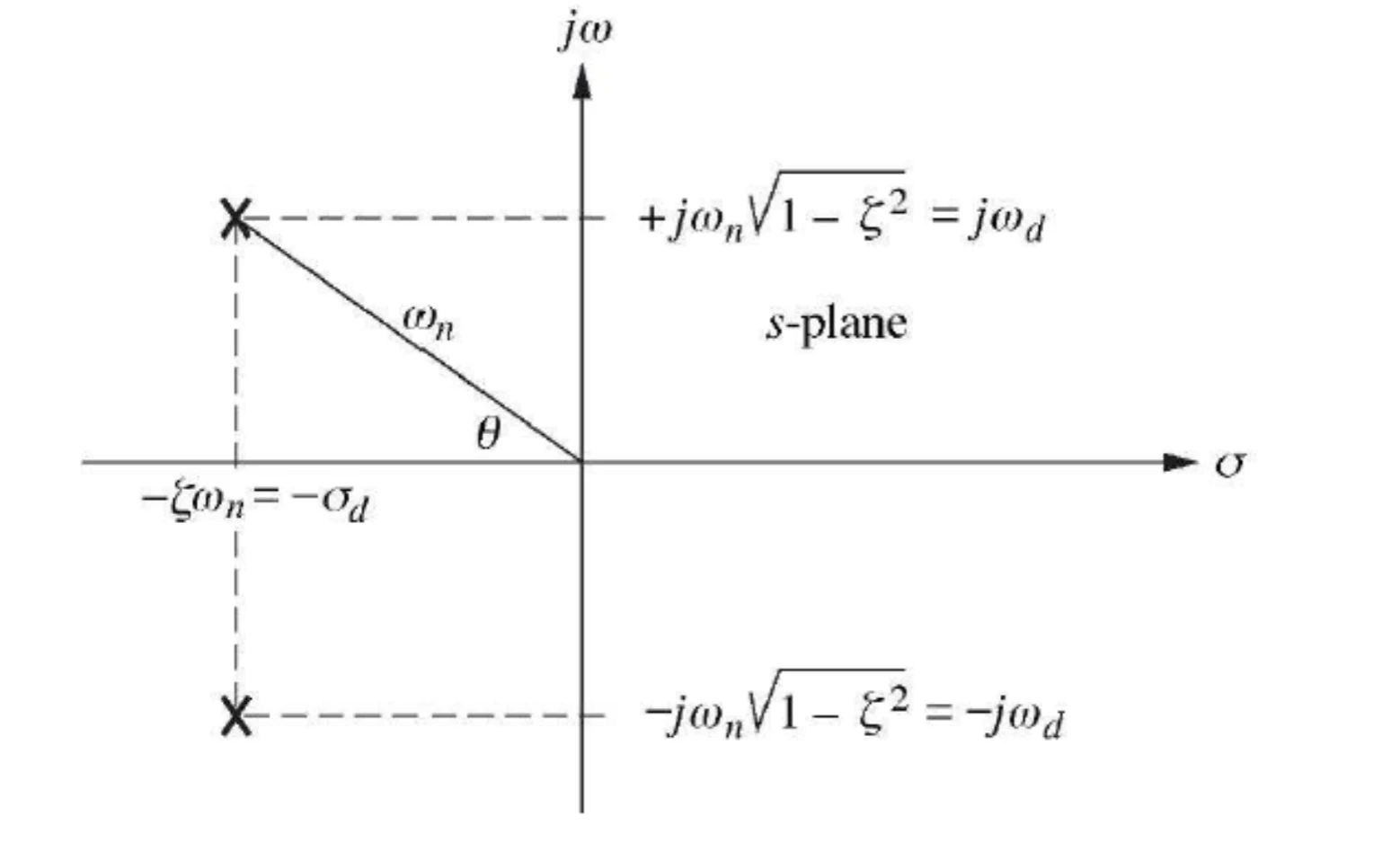poles of second-order underdamped system]] | location of poles | response | examples | | ----------------- | ------------------------------------------------------------------------------ | ---------------------------------------------------------------------------------------- | | Same envelope | ![[thoughts/university/twenty-four-twenty-five/sfwr-4aa4/same-envelope.webp]] | [[thoughts/university/twenty-four-twenty-five/sfwr-4aa4/system response#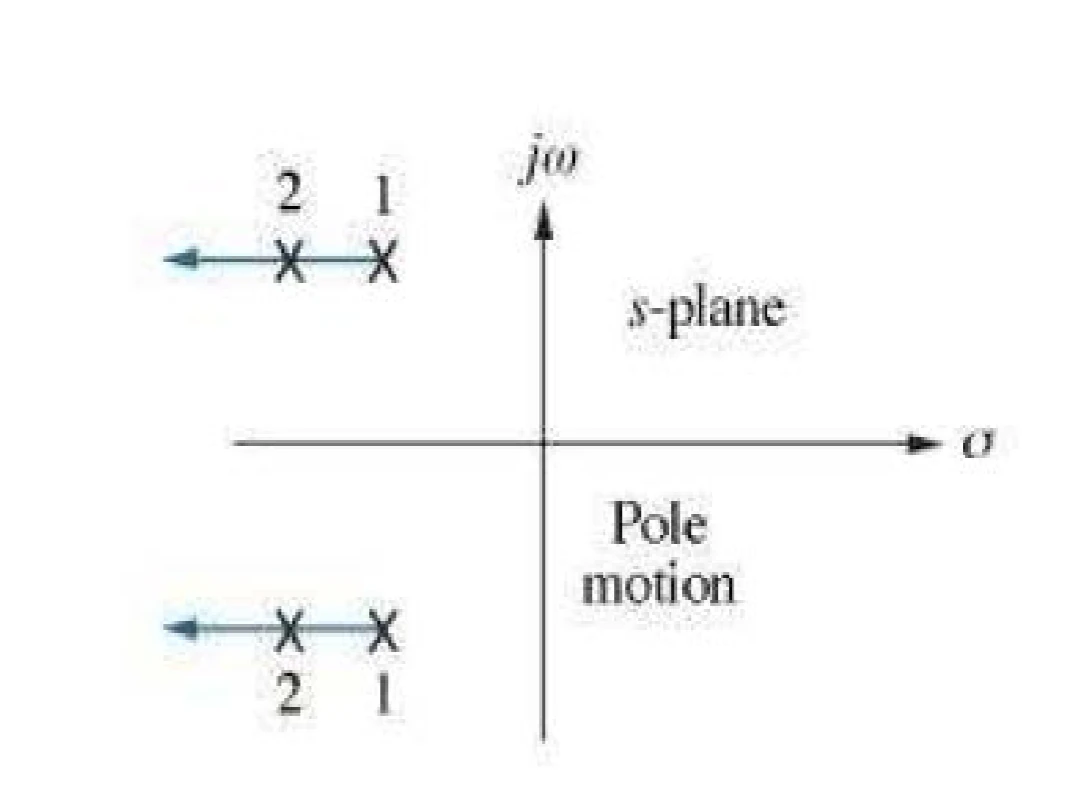same envelope]] | | Same frequency | ![[thoughts/university/twenty-four-twenty-five/sfwr-4aa4/same-frequency.webp]] | [[thoughts/university/twenty-four-twenty-five/sfwr-4aa4/system response#same frequency]] | | Same overshoot | ![[thoughts/university/twenty-four-twenty-five/sfwr-4aa4/same-overshoot.webp]] | [[thoughts/university/twenty-four-twenty-five/sfwr-4aa4/system response#same overshoot]] | #### same envelope
"\\usepackage{tikz}\n\\usepackage{pgfplots}\n\\pgfplotsset{compat=1.16}\n\n\\begin{document}\n\\begin{tikzpicture}\n \\begin{axis}[\n width=12cm, height=8cm,\n xlabel={$t$ (time)},\n ylabel={Amplitude},\n grid=major,\n legend style={at={(0.5,1.1)}, anchor=north, legend columns=-1},\n xmin=0, xmax=10,\n ymin=-1.2, ymax=1.2\n ]\n % First Transfer Function (Sinusoidal)\n \\addplot[blue, thick, samples=100, domain=0:10]\n {exp(-0.1*x)*sin(deg(2*pi*0.5*x))};\n\n % Second Transfer Function (Envelope with Different Frequency)\n \\addplot[red, dashed, thick, samples=100, domain=0:10]\n {exp(-0.1*x)*sin(deg(2*pi*0.8*x))};\n\n % Envelope (Exponential Decay)\n \\addplot[black, dotted, thick, samples=100, domain=0:10]\n {exp(-0.1*x)};\n\n \\addplot[black, dotted, thick, samples=100, domain=0:10]\n {-exp(-0.1*x)};\n \\end{axis}\n\\end{tikzpicture}\n\\end{document}"tikz diagram
source code
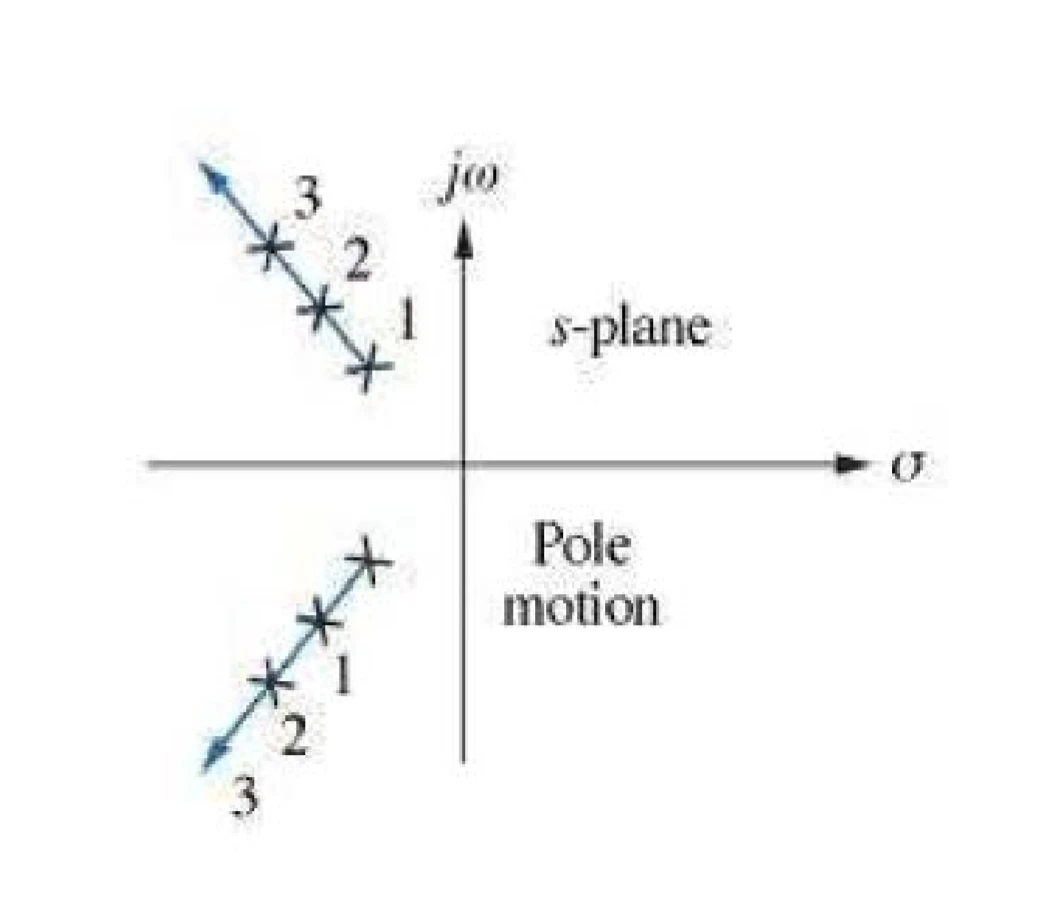
#### same frequency
"\\usepackage{tikz}\n\\usepackage{pgfplots}\n\\pgfplotsset{compat=1.16}\n\n\\begin{document}\n\\begin{tikzpicture}\n \\begin{axis}[\n width=12cm, height=8cm,\n xlabel={$t$ (time)},\n ylabel={Amplitude},\n grid=major,\n legend style={at={(0.5,1.1)}, anchor=north, legend columns=-1},\n xmin=0, xmax=10,\n ymin=-3, ymax=3\n ]\n % First Transfer Function (Higher Amplitude)\n \\addplot[blue, thick, samples=100, domain=0:10]\n {2*sin(deg(2*pi*0.5*x))};\n\n % Second Transfer Function (Lower Amplitude)\n \\addplot[red, dashed, thick, samples=100, domain=0:10]\n {1*sin(deg(2*pi*0.5*x))};\n \\end{axis}\n\\end{tikzpicture}\n\\end{document}"tikz diagram
source code
#### same overshoot
"\\usepackage{tikz}\n\\usepackage{pgfplots}\n\\pgfplotsset{compat=1.16}\n\n\\begin{document}\n\\begin{tikzpicture}\n \\begin{axis}[\n width=12cm, height=8cm,\n xlabel={Time $t$},\n ylabel={Response},\n grid=major,\n legend style={at={(0.5,1.1)}, anchor=north, legend columns=-1},\n xmin=0, xmax=10,\n ymin=0, ymax=2\n ]\n % First System Response\n \\addplot[blue, thick, samples=200, domain=0:10]\n {1 - exp(-0.5*x)*(cos(deg(2*pi*0.5*x)) + 0.1*sin(deg(2*pi*0.5*x)))};\n\n % Second System Response (Same Overshoot, Different Natural Frequency)\n \\addplot[red, dashed, thick, samples=200, domain=0:10]\n {1 - exp(-1*x)*(cos(deg(2*pi*1*x)) + 0.05*sin(deg(2*pi*1*x)))};\n\n % Reference Line for Steady-State Response\n \\addplot[black, dotted, thick] coordinates {(0,1) (10,1)};\n \\end{axis}\n\\end{tikzpicture}\n\\end{document}"tikz diagram
source code