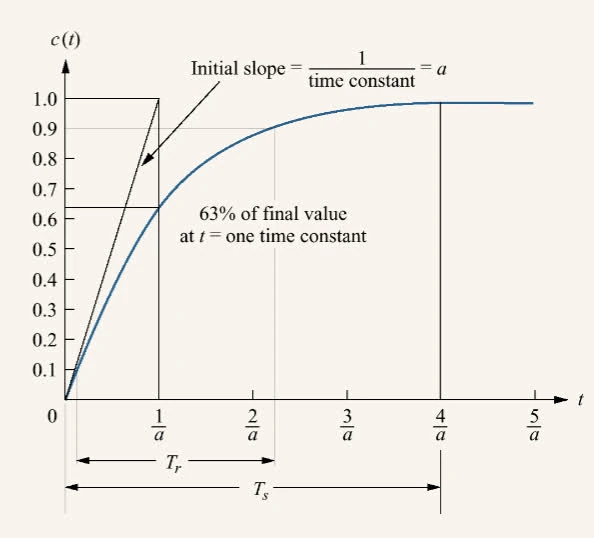
Time response
first order.
second order.
G(s)=s2+as+bb
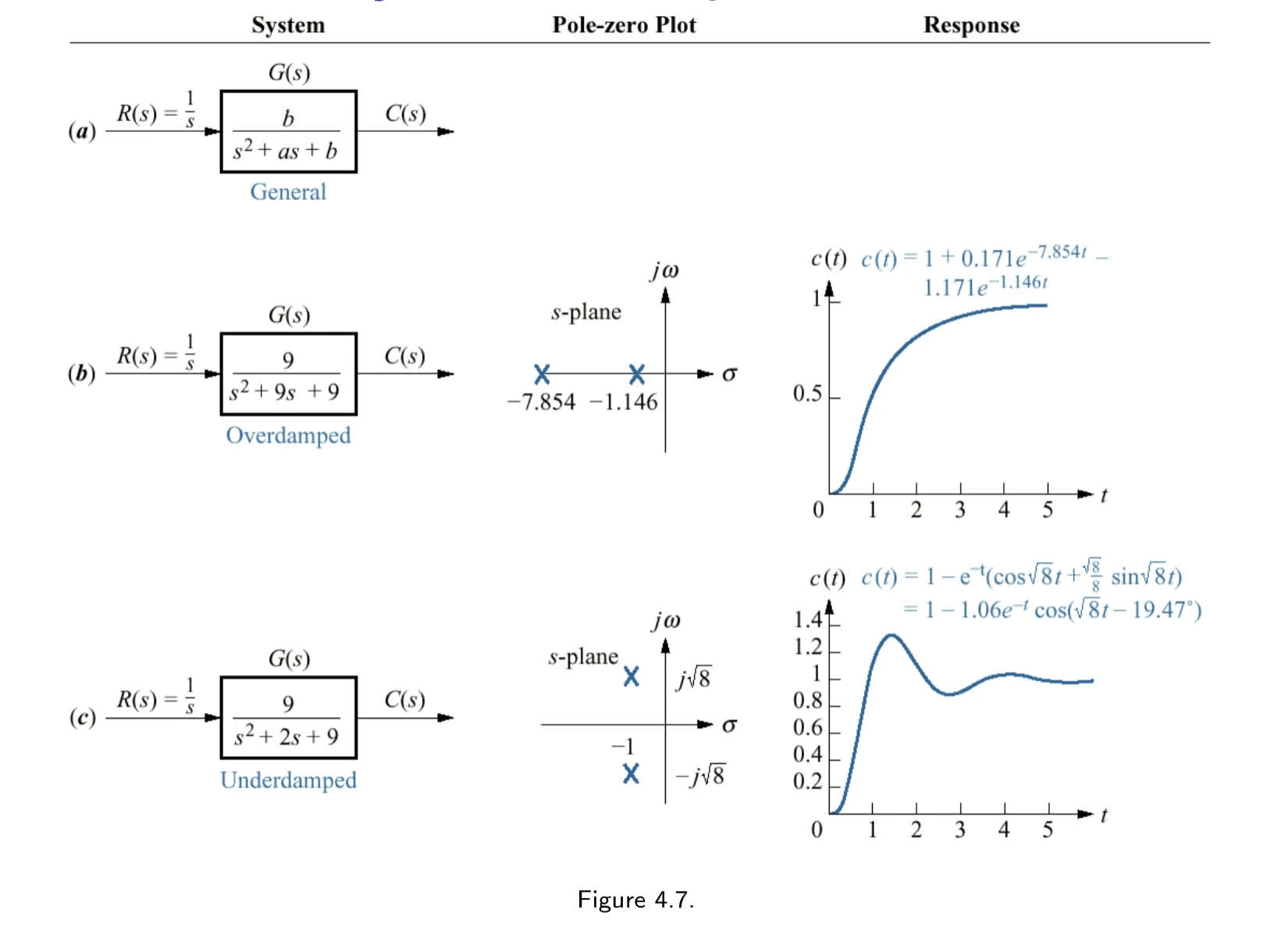 C(s)=s(s2+9s+9)9
C(s)=s(s2+9s+9)9
over-damped response.
For inspect of poles, form of system’s response
c(t)=K1+K2e−σ1t+K3e−σ2t
critically damped response.
System’s response:
c(t)=K1+K2e−σ1t+K3te−σ2t
where −σ1=−3 is our pole location.
under-damped response.
Unit step response to the system:
C(s)=sK1+s+1+j8α+jβ+s+1−j8α−jβ
Thus the form of system’s response:
c(t)=K1+e−σdt[2αcosωdt+2βsinωdt]
e−σdt[2αcosωdt+2βsinωdt]=K4e−σdtcos(ωdt−ϕ)
where ϕ=tan−1(αβ) and K4=(2α)2+(2β)2
general second-order systems
- nature frequency ωn: frequency of oscillation of the system
- damping ratio ζ=natural frequency (rad/sec)exponential decay frequency
Deriving ζ:
- For under-damped system, the poles are σ=2−a
%OS (percent overshoot)
%OS=eζπ/1−ζ2×100%
