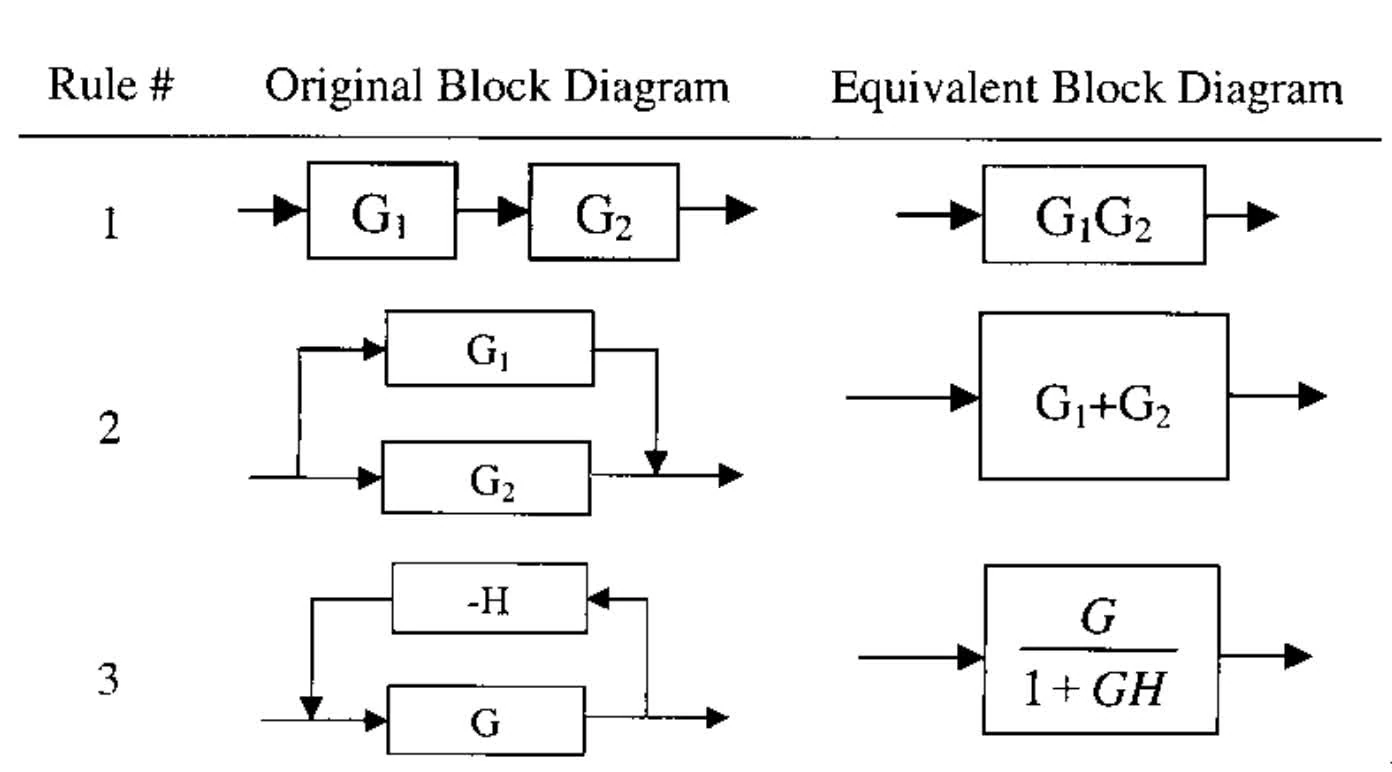
Tout ce qu'il faut savoir sur la conception des systèmes de contrôle See also
Book:
sp.Heaviside(t) is u ( t ) u(t) u ( t )
import sympy import sympy as sp from symbol import symbols , apart , inverse_laplace_transform , simplify from sympy . abc import s , t
See
Transfer function n t h n^{th} n t h linear, time-invariant (LTI) differential equation:
a n d n c ( t ) d t n + a n − 1 d n − 1 c ( t ) d t n − 1 + ⋯ + a 0 c ( t ) = b m d m r ( t ) d t m + b m − 1 d m − 1 r ( t ) d t m − 1 + ⋯ + b 0 r ( t ) a_n \frac{d^n c(t)}{dt^n} + a_{n-1} \frac{d^{n-1} c(t)}{dt^{n-1}} + \cdots + a_0 c(t) = b_m \frac{d^m r(t)}{dt^m} + b_{m-1} \frac{d^{m-1} r(t)}{dt^{m-1}} + \cdots + b_0 r(t) a n d t n d n c ( t ) + a n − 1 d t n − 1 d n − 1 c ( t ) + ⋯ + a 0 c ( t ) = b m d t m d m r ( t ) + b m − 1 d t m − 1 d m − 1 r ( t ) + ⋯ + b 0 r ( t ) takes Laplace transform from both side
a n s n C ( s ) + a n − 1 s n − 1 C ( s ) + ⋯ + a 0 C ( s ) and init terms for c ( t ) = b m s m R ( s ) + b m − 1 s m − 1 R ( s ) + ⋯ + b 0 R ( s ) and init terms for r ( t ) \begin{aligned}
& a_n s^n C(s) + a_{n-1} s^{n-1} C(s) + \cdots + a_0 C(s) \text{ and init terms for } c(t) \\
& = b_m s^m R(s) + b_{m-1} s^{m-1} R(s) + \cdots + b_0 R(s) \text{ and init terms for } r(t) \\
\end{aligned} a n s n C ( s ) + a n − 1 s n − 1 C ( s ) + ⋯ + a 0 C ( s ) and init terms for c ( t ) = b m s m R ( s ) + b m − 1 s m − 1 R ( s ) + ⋯ + b 0 R ( s ) and init terms for r ( t ) assume initial conditions are zero
( a n s n + a n − 1 s n − 1 + ⋯ + a 0 ) C ( s ) = ( b m s m + b m − 1 s m − 1 + ⋯ + b 0 ) R ( s ) C ( s ) R ( s ) = G ( s ) = b m s m + b m − 1 s m − 1 + ⋯ + b 0 a n s n + a n − 1 s n − 1 + ⋯ + a 0 \begin{aligned}
(a_n s^n + a_{n-1} s^{n-1} + \cdots + a_0)C(s) &= (b_m s^m + b_{m-1} s^{m-1} + \cdots + b_0)R(s) \\[8pt]
\frac{C(s)}{R(s)} &= G(s) = \frac{b_m s^m + b_{m-1} s^{m-1} + \cdots + b_0}{a_n s^n + a_{n-1} s^{n-1} + \cdots + a_0}
\end{aligned} ( a n s n + a n − 1 s n − 1 + ⋯ + a 0 ) C ( s ) R ( s ) C ( s ) = ( b m s m + b m − 1 s m − 1 + ⋯ + b 0 ) R ( s ) = G ( s ) = a n s n + a n − 1 s n − 1 + ⋯ + a 0 b m s m + b m − 1 s m − 1 + ⋯ + b 0
G ( s ) = C ( s ) R ( s ) G(s)=\frac{C(s)}{R(s)} G ( s ) = R ( s ) C ( s )
Q: G ( s ) = 1 S + 2 G(s) = \frac{1}{S+2} G ( s ) = S + 2 1 u ( t ) u(t) u ( t ) y ( t ) y(t) y ( t )
Y ( s ) = G ( s ) ⋅ u ( s ) → Y ( s ) = 1 s ( s + 2 ) = A s + B s + 2 = 1 2 ⋅ s − 1 2 ⋅ ( s + 2 ) y ( t ) = − 1 2 ( 1 − e − 2 t ) u ( t ) \begin{aligned}
Y(s) &= G(s)\cdot u(s) \rightarrow Y(s)=\frac{1}{s(s+2)} = \frac{A}{s} + \frac{B}{s+2} = \frac{1}{2\cdot{s}} - \frac{1}{2\cdot{(s+2)}} \\
y(t) &= -\frac{1}{2}(1-e^{-2t})u(t)
\end{aligned} Y ( s ) y ( t ) = G ( s ) ⋅ u ( s ) → Y ( s ) = s ( s + 2 ) 1 = s A + s + 2 B = 2 ⋅ s 1 − 2 ⋅ ( s + 2 ) 1 = − 2 1 ( 1 − e − 2 t ) u ( t ) Transfer function with feedback is under form
G ( s ) 1 + G ( s ) H ( s ) \frac{G(s)}{1+G(s)H(s)} 1 + G ( s ) H ( s ) G ( s ) Equivalent Resistance and Impedance x ˙ = A x + B u y = C x + D u \begin{align*}
\dot{x} &= Ax + Bu \\
y &= Cx + Du
\end{align*} x ˙ y = A x + B u = C x + D u Given
G ( s ) = ∑ i = 1 n − 1 b i s i + b 0 s n + ∑ i = 1 n − 1 a i s i + a 0 = Y ( s ) U ( s ) G(s) = \frac{\sum_{i=1}^{n-1}b_is^i + b_{0}}{s^n + \sum_{i=1}^{n-1}a_is^{i} + a_{0}} = \frac{Y(s)}{U(s)} G ( s ) = s n + ∑ i = 1 n − 1 a i s i + a 0 ∑ i = 1 n − 1 b i s i + b 0 = U ( s ) Y ( s ) We get controller canonical state space form:
x ˙ ( t ) = [ 0 1 0 ⋯ 0 0 0 0 1 ⋯ 0 0 ⋮ ⋮ ⋮ ⋱ ⋮ ⋮ 0 0 0 ⋯ 1 0 0 0 0 ⋯ 0 1 − a 0 − a 1 − a 2 ⋯ − a n − 2 − a n − 1 ] x ( t ) + [ 0 0 ⋮ 0 0 1 ] u ( t ) y ( t ) = [ b 0 b 1 ⋯ b n − 2 b n − 1 ] x ( t ) . \begin{aligned}
\dot{x}(t) &= \begin{bmatrix}
0 & 1 & 0 & \cdots & 0 & 0 \\\
0 & 0 & 1 & \cdots & 0 & 0 \\\
\vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\\
0 & 0 & 0 & \cdots & 1 & 0 \\\
0 & 0 & 0 & \cdots & 0 & 1 \\\
-a_0 & -a_1 & -a_2 & \cdots & -a_{n-2} & -a_{n-1}
\end{bmatrix} x(t) + \begin{bmatrix}
0 \\\
0 \\\
\vdots \\\
0 \\\
0 \\\
1
\end{bmatrix} u(t) \\\
y(t) &= \begin{bmatrix}
b_0 & b_1 & \cdots & b_{n-2} & b_{n-1}
\end{bmatrix} x(t).
\end{aligned} x ˙ ( t ) y ( t ) = 0 0 ⋮ 0 0 − a 0 1 0 ⋮ 0 0 − a 1 0 1 ⋮ 0 0 − a 2 ⋯ ⋯ ⋱ ⋯ ⋯ ⋯ 0 0 ⋮ 1 0 − a n − 2 0 0 ⋮ 0 1 − a n − 1 x ( t ) + 0 0 ⋮ 0 0 1 u ( t ) = [ b 0 b 1 ⋯ b n − 2 b n − 1 ] x ( t ) . We get observer canonical state space form:
x ˙ ( t ) = [ − a n − 1 1 0 ⋯ 0 0 − a n − 2 0 1 ⋯ 0 0 ⋮ ⋮ ⋮ ⋱ ⋮ ⋮ − a 2 0 0 ⋯ 1 0 − a 1 0 0 ⋯ 0 1 − a 0 0 0 ⋯ 0 0 ] x ( t ) + [ b n − 1 b n − 2 ⋮ b 2 b 1 b 0 ] u ( t ) y ( t ) = [ 1 0 ⋯ 0 0 ] x ( t ) . \begin{aligned} \dot{x}(t) &= \begin{bmatrix} -a_{n-1} & 1 & 0 & \cdots & 0 & 0 \\ -a_{n-2} & 0 & 1 & \cdots & 0 & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ -a_2 & 0 & 0 & \cdots & 1 & 0 \\ -a_1 & 0 & 0 & \cdots & 0 & 1 \\ -a_0 & 0 & 0 & \cdots & 0 & 0 \end{bmatrix} x(t) + \begin{bmatrix} b_{n-1} \\ b_{n-2} \\ \vdots \\ b_2 \\ b_1 \\ b_0 \end{bmatrix} u(t) \\ y(t) &= \begin{bmatrix} 1 & 0 & \cdots & 0 & 0 \end{bmatrix} x(t). \end{aligned} x ˙ ( t ) y ( t ) = − a n − 1 − a n − 2 ⋮ − a 2 − a 1 − a 0 1 0 ⋮ 0 0 0 0 1 ⋮ 0 0 0 ⋯ ⋯ ⋱ ⋯ ⋯ ⋯ 0 0 ⋮ 1 0 0 0 0 ⋮ 0 1 0 x ( t ) + b n − 1 b n − 2 ⋮ b 2 b 1 b 0 u ( t ) = [ 1 0 ⋯ 0 0 ] x ( t ) . See
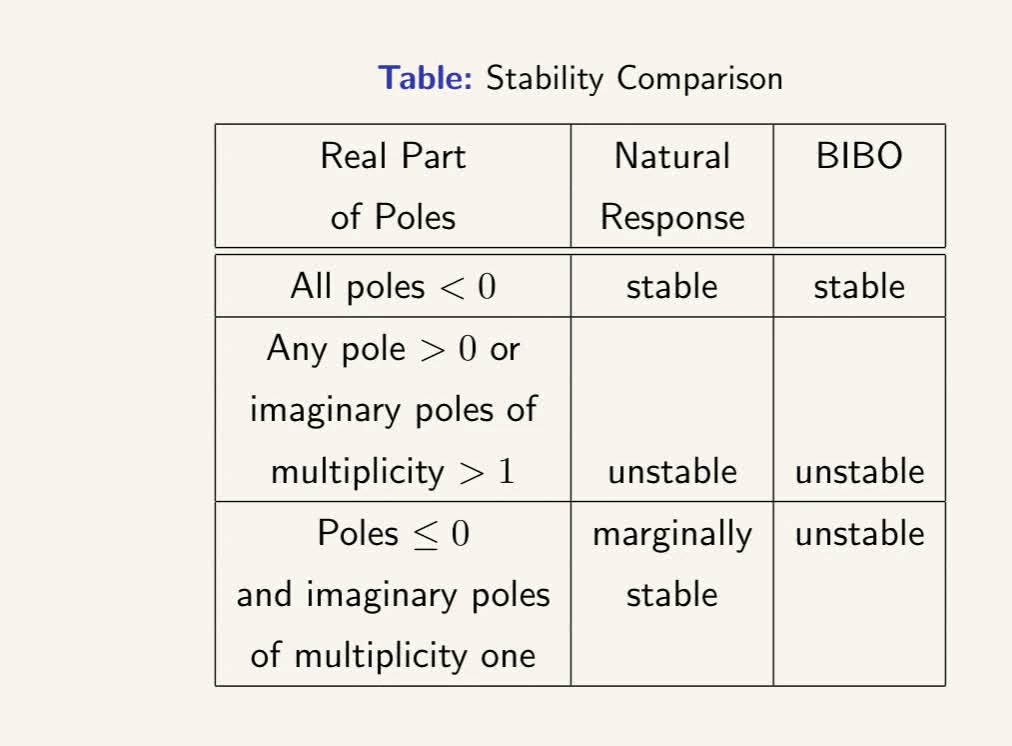
Necessary and sufficient condition for stability
to have all roots in open left hand plane is to have all coefficients of polynomial to be present and have same sign.
To find transfer function for a system given a step response graph, *look for time over around 63% of the final value$
Closed-loop transfer function
T ( s ) = G ( s ) 1 + G ( s ) T(s) = \frac{G(s)}{1+G(s)} T ( s ) = 1 + G ( s ) G ( s )
%OS (percent overshoot) % O S = e ζ π / 1 − ζ 2 × 100 % \%OS = e^{\zeta \pi / \sqrt{1-\zeta^2}} \times 100 \% % OS = e ζ π / 1 − ζ 2 × 100% If a unity feedback system has a feedforward transfer function G ( s ) G(s) G ( s ) E ( s ) R ( s ) \frac{E(s)}{R(s)} R ( s ) E ( s )
C ( s ) = E ( s ) ⋅ G ( s ) E ( s ) = R ( s ) − C ( s ) \begin{aligned}
C(s) &= E(s)\cdot G(s) \\\
E(s) &= R(s) - C(s)
\end{aligned} C ( s ) E ( s ) = E ( s ) ⋅ G ( s ) = R ( s ) − C ( s ) For G ( s ) = K G(s) = K G ( s ) = K E ( s ) R ( s ) = 1 1 + G ( s ) \frac{E(s)}{R(s)} = \frac{1}{1+G(s)} R ( s ) E ( s ) = 1 + G ( s ) 1
state space design Closed-loop system characteristic equation
d e t ( S I − ( A − B K ) ) det(SI - (A-BK)) d e t ( S I − ( A − B K )) Gain and Phase Stability Margins Closed loop pole exists when
1 + K G ( s ) H ( s ) = 0 1+KG(s)H(s) = 0 1 + K G ( s ) H ( s ) = 0 zero order hold Nyqust frequency:
f N = 1 2 f s f_N = \frac{1}{2}f_s f N = 2 1 f s Set the third pole to s=-2 to cancel a zero as third pole.
